Dalam bidang geometri pemahaman mengenai pengertian garis, titik, bidang, dan ruang merupakan konsep dasar dari materi terkait lainnya. Hal ini selalu digunakan dalam konsep dasar materi bangun datar dan bangun ruang. Selain itu, ini juga digunakan di bidang ilmu lain seperti seni musik.
A. Pengertian Titik
Secara umum, titik adalah simbol yang mewakili suatu keadaan tertentu (Oxford Dictionary) yang digambarkan sebagai lingkaran kecil berwarna. Titik merupakan sebuah tipografi atau metode penulisan yang tidak didefinisikan secara mengkhusus. Berikut, pengertian titik terkait ilmu yang digunakan:
- Dalam ilmu bahasa, titik (dot) adalah simbol yang dapat mewakili keadaan tertentu dalam suatu konteks penulisan. Misalnya: tanda titik untuk mengakhiri kalimat, tanda 3 titik untuk membuat pertanyaan lisan, tanda titik-titik untuk menulis teriakan, dan lain-lain.
- Dalam ilmu matematika, titik (point) adalah unsur yang mewakili suatu lokasi namun tidak mempunyai panjang, lebar, dan tinggi. Titik dalam ilmu matematika disimbolkan dengan tanda titik (dot).
- Dalam ilmu seni musik, titik adalah suatu tanda yang digunakan untuk penambahan panjang suatu ketukan nada.
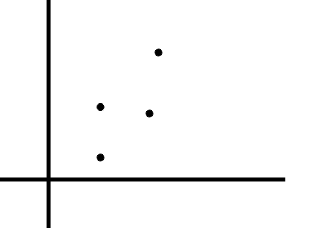
Secara geometri, titik dapat diidentifikasi sebagai sebuah huruf misalnya titik A, titik B, dan lain-lain. Untuk mempermudah identifikasi titik dalam koordinat kartesius, titik dapat memuat keterangan misalnya A (x,y), dengan x adalah posisi dalam sumbu x dan y adalah posisi dalam sumbu y. Nama sumbu x disebut juga absis dan sumbu y disebut juga ordinat.
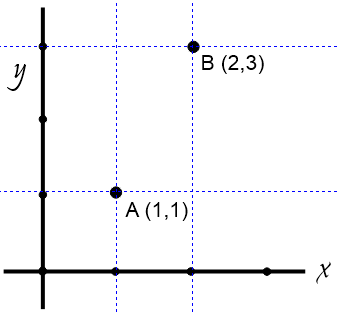
Contoh di atas titik A (1,1) karena berada dalam posisi 1 pada koordinat absis (sumbu x) dan posisi 1 pada ordinat (sumbu y).
Contoh di atas titik B (2,3) karena berada dalam posisi 2 pada koordinat absis (sumbu x) dan posisi 3 pada ordinat (sumbu y).
B. Pengertian Garis
Dalam bidang geometri, garis adalah himpunan titik-titik yang terhubung secara kontinu (berjejer lurus atau melengkung) yang hanya mempunyai satu titik akhir dan satu titik awal. Penamaan garis umumnya menggunakan 2 huruf yang menunjukkan titik awal dan titik akhir. Misalnya garis AB di bawah ini,
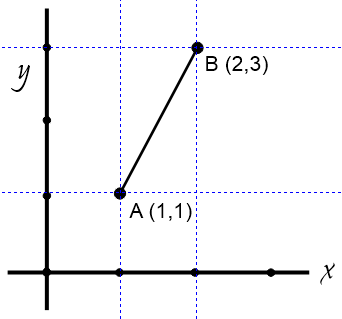
Garis AB pada koordinat kartesius merupakan perpanjangan titik A dan B yang membentuk garis lurus. Garis mempunyai unsur dimensi panjang yang dapat diukur secara langsung atau menggunakan rumus jarak. Karena garis yang terbentuk adalah garis lurus, dapat dihitung dengan rumus euclidean pada R² (ruang dimensi 2) yaitu sebagai berikut,
d = jarak atau panjang garis lurus
x1, x2 = posisi masing-masing titik pada sumbu x
y1, y2 = posisi masing-masing titik pada sumbu y
Misalkan A (x1, y1) dan B (x2, y2), dapat diperoleh
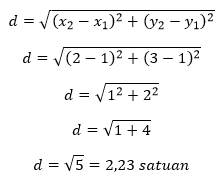
Garis tidak hanya berbentuk lurus terdapat pula garis-garis yang berbentuk lengkung seperti gambar berikut,

C. Pengertian Bidang
Bidang adalah permukaan datar yang mempunyai bentuk 2 dimensi sehingga dapat diukur panjang dan lebarnya. Bidang merupakan perluasan dari garis-garis yang terhubung menjadi satu permukaan datar. Misalnya bidang ABC berikut,
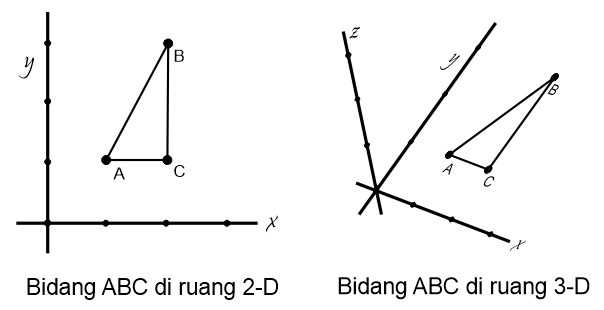
Bidang datar memuat unsur-unsur yang lebih kompleks dari garis dan titik, tergantung bentuk bidang. Berikut bentuk-bentuk bidang yang umum dipelajari, yaitu:
D. Pengertian Ruang
Dalam konsep matematika kuno, ruang adalah bentuk dari bangun 3 dimensi yang ada dalam kehidupan sehari-hari dan memiliki unsur panjang, lebar, dan tinggi. Sama halnya dengan titik, garis, dan bidang; konsep ruang merupakan sebuah aksioma dalam ilmu matematika, karena dapat terbukti dengan sendirinya. Konsep ini telah diteliti oleh Euklides (matematikawan Mesir, ± 300 sebelum masehi). Sebagai contoh populer, bangun piramida merupakan bukti kebesaran peradaban mesir kuno di bidang geometri. Berikut contoh bangun ruang dalam ruang euclidean di R³ (ruang dimensi 3),
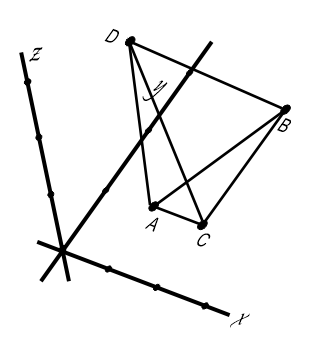
Bangun memuat unsur-unsur yang lebih kompleks dari bangun datar, tergantung bentuknya. Berikut bentuk-bentuk bangun ruang yang umum dipelajari, yaitu:
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel “Pengertian Garis Titik Bidang dan Ruang beserta Contohnya”. Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih…











