Sifat-sifat garis di bidang geometri ditentukan oleh kedudukannya terhadap garis lainnya, yang terdiri dari garis sejajar, garis berpotongan, garis tegak lurus, dan garis berimpit. Berikut akan dijelaskan ke-4 sifat kedudukan antar garis tersebut.
Artikel terkait: Pengertian Garis Titik Bidang dan Ruang beserta Contohnya
A. Garis Sejajar
Garis sejajar adalah suatu kedudukan dua garis pada bidang datar yang tidak mempunyai titik potong walaupun kedua garis diperpanjang. Secara geometri kesejajaran garis tidak akan pernah bertemu satu dengan lainnya karena mempunyai kemiringan (gradien) yang sama. Garis-garis sejajar tidak harus sama panjang.
Contoh garis sejajar:
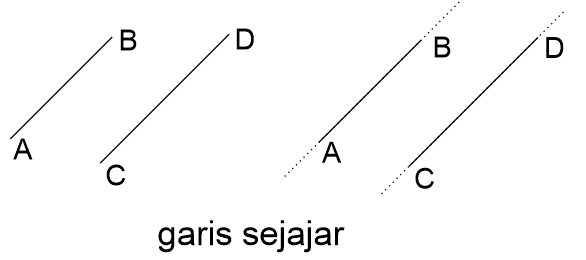
Contoh garis tidak sejajar:
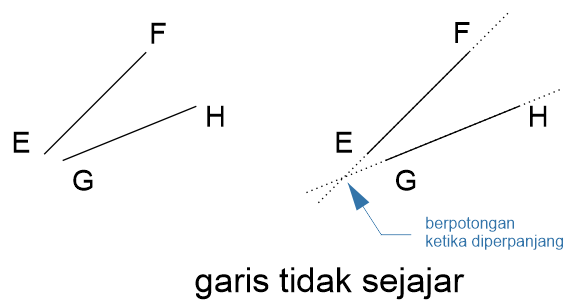
B. Garis Berpotongan
Garis berpotongan adalah kedudukan dua garis yang mempunyai titik potong karena kedua garis saling bertemu. Secara geometri garis-garis yang berpotongan terjadi karena mempunyai kemiringan yang berbeda dan panjang antar garis memungkinkan untuk saling bertemu. Garis yang berpotongan sudah pasti tidak sejajar, namun garis tidak sejajar belum tentu berpotongan.
Contoh garis berpotongan:
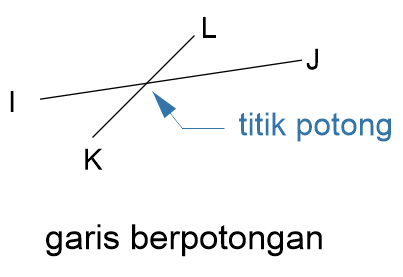
C. Garis Tegak Lurus
Garis tegak lurus adalah kedudukan garis yang berpotongan dan pada titik potongnya terbentuk sudut siku-siku (90°). Garis tegak lurus juga disebut dengan garis serenjang atau garis perpendikular. Dalam simbol matematika garis tegak lurus disimbolkan dengan simbol perpendikular "⊥", misalnya garis MN tegak lurus dengan OP dapat ditulis MN ⊥ OP.
Contoh garis tegak lurus:
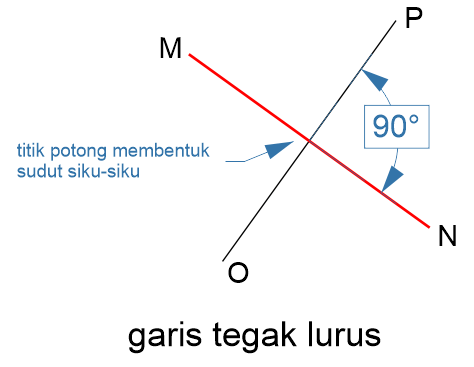
Perkalian dua kemiringan (gradien) garis tegak lurus adalah -1 atau memenuhi persamaan M1 × M2 = -1.
Jika, M1 = a/b maka M2 = - b/a * Karena berlaku M1 × M2 = a/b × (- b/a) = - ab/ab = -1 Contoh: Kemiringan garis MN adalah M1 = 2/3, berapakah kemiringan garis OP di atas? Penyelesaian: Karena garis OP ⊥ NM maka gradien garis OP = M2 dihitung memenuhi persamaan M1 × M2 = a/b × (- b/a) = -1 M1 = a/b = 2/3 a = 2 b = 3 M2 = - b/a = - 3/2 Jadi, gradien garis OP adalah - 3/2
D. Garis Berimpit
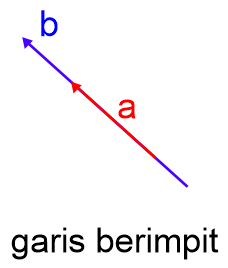
Garis berimpit adalah kedudukan garis yang saling menutupi antara satu dengan lainnya, sehingga garis berimpit tidak dapat dilihat dengan kasat mata. Garis berimpit dapat terjadi karena posisi garis yang sama, namun 2 garis berimpit belum tentu mempunyai panjang yang sama.
Contoh garis berimpit:
Baca juga tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel "Pengertian Garis Sejajar, Garis Berpotongan, Tegak Lurus, dan Berimpit". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih…












Makasih banyak,,,,,,,,,,,,,karena ini aq lngsng paham>_<
Sama-sama Eka Kartika Ayu... Terima kasih juga atas komentarnya 🙂
Kak, apakah garis berimpit memungkinkan untuk berbeda arah? Trimakasih.
Garis berimpit memungkinkan untuk berbedah arah kak Andy, misalnya arah barat dan arah timur.
Semoga membantu 🙂
Kak kemungkinan ada jenis garis lagi gak
Ada dik, misalnya garis linear, garis non-linier, garis putus-putus.
Semoga bermanfaat 🙂
Ka kalo dua garis yg posisinya sama dinamakan garis sejajar atau garis berimpit ??
Hai Dani,
Dua garis pada posisi yang sama disebut garis berimpit.
Semoga membantu 🙂
Garis sejajar panjangnya harus sama atau tidak?
Hai Reza garis sejajar tidak harus sama panjang. Sebenarnya secara geometri, garis sejajar disebut dengan garis "parallel". Namun, jarak antar titik-titik di garis 1 dan 2 saat ditelusuri harus sama panjang, istilah ini disebut dengan "equidistant" pada garis sejajar.
Untuk kasus lain, garis sejajar juga tidak harus lurus, garis sejajar juga boleh bengkok, yang terpenting mempunyai equidistant yang sama, misalnya: kurva sejajar.
Juga, untuk tingkat pembelajaran lanjutan yaitu "vektor sejajar" pun juga tidak harus sama panjang
Semoga membantu 🙂
Makasih karna jawaban ini aku juara 1 Aulia
Terima kasih gara gara google saya bisa jadi giat belajar semoga google setiap hari banyak yang menggunakannya
TERIMA KASIH GOOGLE.MEMANG YANG TERBAIK BAI 😘😗
Hai Nabila
Iya Google emang baik, terima kasih juga buat Google 🙂
Hai kak aku mau tanya
Contoh lain gambar garis berhimpitan..
Hai Alif Zuhdi Qardhawi,
Garis berimpit hanya seperti garis lurus umumnya, contoh lainnya: 3 garis berimpit misalnya, dengan masing-masing garis mempunyai warna berbeda.
Semoga bermanfaat 🙂
Ka apa rumus gradien 2 buah berpotongan?
Hai Akhmadzulkarnai,
Dua garis berpotongan mempunyai gradien memenuhi persamaan M1 × M2 = a/b × (- b/a) = -1
Jika, M1 = a/b maka M2 = - b/a
Semoga bermanfaat 🙂
Kak mau tanya sifat-sifat garis tegak lurus apa² sajakah?
Hai Khalisah Azzahrah, Sifat umum dua atau lebih garis disebut tegak lurus:
* Membentuk Titik Potong
* sudut siku-siku (90°)
Semoga membantu 🙂
Kak . contoh benda disekitar kita yang memiliki garis sejajar atau garis berpotongan apa ya
Hai salsabila, kakak mencoba membantu
Garis sejajar: Senar gitar, rel kereta api, roller coaster, zebra cross, penggaris, Tv, buku, kardus, dll
garis berpotongan: kincir angin, baling-baling, kawat penyaring, perempatan jalan, dll
Semoga membantu 🙂
Terima kasi ini sangat membantu
Hai Adji, terima kasih kembali 🙂
Kak apa yang dimaksud dengan garis sejajar , garis berpotongan , dan garis berimpit
Hai Muhammad Syaifudin.
* garis sejajar: suatu kedudukan dua garis pada bidang datar yang tidak mempunyai titik potong walaupun kedua garis diperpanjang.
* garis berpotongan: kedudukan dua garis yang mempunyai titik potong karena kedua garis saling bertemu.
* garis berimpit: kedudukan garis yang saling menutupi antara satu dengan lainnya, sehingga garis berimpit tidak dapat dilihat dengan kasat mata.
* garis tegak lurus: kedudukan garis yang berpotongan dan pada titik potongnya terbentuk sudut siku-siku (90°)
Lebih jelasnya silakan baca artikel di atas.
Semoga bermanfaat 🙂
kak mau tanya kalau kubus dan balok mempunyai berapa garis potong ya?
Hai nia, Kubus dan balok dapat membentuk garis berpotongan di antara diagonal ruangnya atau pun diagonal sisinya
Untuk lebih lanjut dapat membaca artikel Kubus
Semoga bermanfaat 🙂
Ok kak...makasih jawabannya🙏
mau nanya ya. apakah garis bersilangan sama dengan garis tegak lurus?
Hai Sevanya, garis bersilangan dan tegak lurus itu berbeda.
Semoga membantu 🙂
Benar atau salah ? Fungsi garis lurus dan garis lengkung akan selalu berpotongan.
Salah, Fungsi garis lurus dan garis lengkung tidak selalu berpotongan,
Ini terbukti dengan teknik pembuktian kontradiksi,
Misalnya garis lurus sejajar sumbu x yang berpotongan di titik y negatif dengan garis lengkung sebagai fungsi kuadrat yang terbuka ke atas dengan titik ekstrim positif; keduanya tidak akan pernah bertemu.
Semoga membantu 🙂
Garis ruas garis saling berhimpit di salah satu ujungny membentuk sebuah
Hai kak Eka putri
Salah satu ujungnya membentuk sudut
Semoga membantu 🙂
kalo dua buah garis yg bertemu pada sebuah titik disebuat apa?
Hai Suci, dua buah garis yang bertemu disebut garis berpotongan
Semoga membantu 🙂
Terimaksih atas ilmu nya;)
Terima kasih kembali Cenzo atas komentarnya
Semoga membantu 🙂
Ka kalo ada garis yang bersilangan maksudnya gimana? Kalau bersilangan kan artinya bisa membentuk huruf x atau +, tapi itu mirip kaya tegak lurus. Yang bener apa ka?
Tegak lurus harus membentuk sudut 90 sederajat (siku-siku), sedangkan bersilangan tidak harus membentuk sudut siku-siku 90 derajat
Semoga membantu Aprilia 🙂
Izin menjawab, untuk mengetahui perbedaan garis tegak lurus dan bersilangan dapat jelas terlihat jika kita mengambar bangun ruang.
Garis tegak lurus terjadi pada SATU bidang datar, sedangkan garis bersilangan terjadi pada DUA bidang datar.
Kalau garis p dan q adalah dua garis yang tidak memiliki titik potong meskipun diperpanjang sampai tak terhingga, kedudukan titik p dan q termasuk apa?
kak bagaimana syarat menemukan dua garis saling berpotongan, dua garis sejajar dan dua garis berimpit?