A. Pengertian Bangun Ruang (3D Geometric Shapes)
Bangun ruang adalah bentuk bangun (struktur objek) di ruang 3 dimensi yang dapat diukur bagian-bagiannya dalam koordinat kartesius di R³, yaitu sumbu-x, sumbu-y, dan sumbu-z. Secara sederhana, bangun ruang merupakan objek yang diukur berdasarkan 3 variabel yaitu: panjang (x), lebar (y), dan tinggi (z). Keberadaannya di ruang 3 dimensi menyebabkan bangun ruang mempunyai volume dan luas permukaan. Berikut beberapa hal penting yang perlu diketahui terkait bangun ruang dan rumusnya.
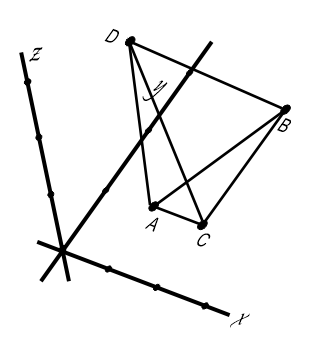
- Bangun ruang dapat diukur melalui koordinat x, y, z di R³ dan memiliki volume, luas permukaan, serta jaring-jaring. Pengukuran bangun ruang menggunakan jarak antar titik di R³. Hal ini diperlukan untuk tingkat pembelajaran yang lebih tinggi terkait geometri analitik.
- Volume bangun ruang adalah banyaknya isi ruang yang digunakan oleh suatu bangun. Satuan yang digunakan yaitu satuan volume, misalnya liter, ml, meter kubik; misalnya dm³ dan cm³.
- Luas permukaan bangun ruang adalah total seluruh luas yang menutupi isi suatu bangun ruang. Luas permukaan suatu bangun ruang ditentukan oleh jaring-jaring-nya. Satuan yang digunakan yaitu satuan luas, misalnya are, hektar, meter kuadrat; misalnya m² dan cm².
- Jaring-jaring bangun ruang adalah bentuk 2-D yang dapat dilipat-lipat hingga membentuk suatu bentuk bangun ruang 3-D. Luas keseluruhan bangun 2-D pada jaring-jaring sama dengan luas permukaan suatu bangun ruang.
- Beberapa bangun ruang, dapat mempunyai definisi ukuran lain. Misalnya, bola mempunyai ukuran diameter yang secara langsung mendefinisikan variabel panjang, lebar, dan tinggi.
Baca juga: Rumus Bangun Datar
B. 8 Jenis dan Rumus Bangun Ruang beserta Contohnya
Berikut jenis-jenis dan rumus bangun ruang yang umum digunakan dalam pembelajaran matematika .Masing-masing contoh soal dapat dibuka melalui tautan yang telah disediakan pada 8 jenis bangun ruang, yaitu: kubus, balok, tabung, kerucut, limas segi tiga, limas segi empat, bola, dan prisma. Untuk mengakses salah satu bangun klik pada navigasi berikut.
Navigasi Cepat
-
Kubus
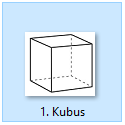
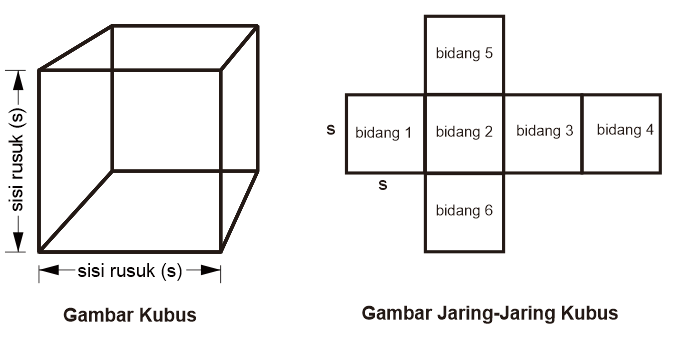
Kubus adalah bangun ruang tiga dimensi yang tersusun dari 6 bidang datar yang kongruen, keenam bidang kongruen pada kubus berbentuk persegi.
Keterangan: s = sisi kubus
Nama Rumus Volume (V) V = s × s × s V = s³ Luas permukaan (L) L = 6 × s × s L = 6 × s² Sisi rusuk (s) Diagonal sisi (ds) Diagonal ruang (dr) Luas bidang diagonal (bd) Artikel terkait: Contoh Soal Kubus
-
Balok
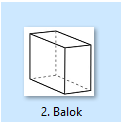
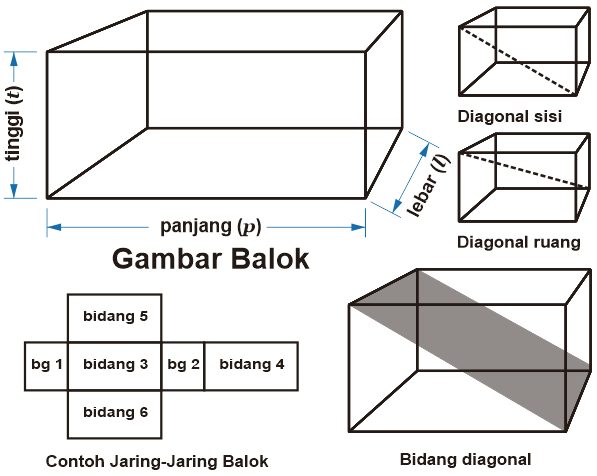
Balok adalah bangun ruang tiga dimensi yang tersusun oleh 3 pasang segi empat (persegi atau persegi panjang) dan paling sedikit mempunyai 1 pasangan sisi segi empat yang mempunyai bentuk yang berbeda.
Keterangan: t = tinggi p = panjang l = lebar
Artikel terkait: Contoh Soal Balok
-
Tabung
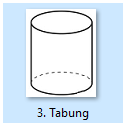
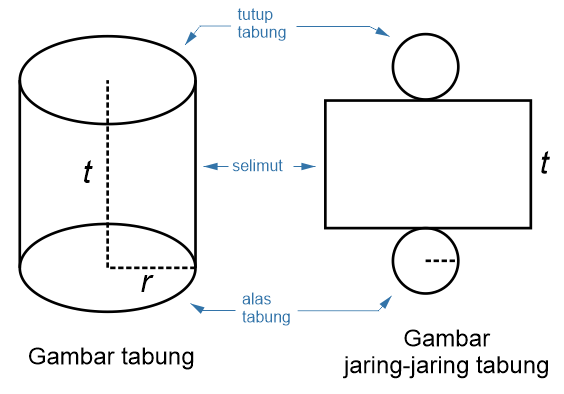
Tabung adalah bangun ruang yang tersusun oleh 3 buah sisi yaitu 2 buah lingkaran yang mempunyai ukuran yang sama dan 1 segiempat yang mengelilingi kedua lingkaran tersebut.
Keterangan: t = tinggi jari-jari (r) = d÷2 diameter (d) = 2×r π = 22/7 untuk jari-jari kelipatan 7 dan 3,14 untuk jari-jari bukan kelipatan 7Artikel terkait: Contoh Soal Tabung
-
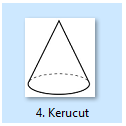
Kerucut
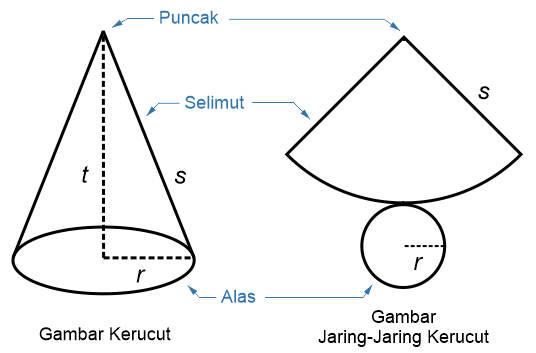
Kerucut adalah bangun ruang yang memiliki 2 sisi yaitu sebuah lingkaran dan sebuah bidang lengkung.
Keterangan: t = tinggi r = jari-jari s = panjang garis pelukis (apotema), merupakan garis yang menghubungkan titik puncak dengan titik keliling alas kerucut. Nilai s dapat dihitung menggunakan rumus Pythagoras.
π = 22/7 untuk jari-jari (r) kelipatan 7 dan 3,14 untuk jari-jari bukan kelipatan 7
Nama Rumus Volume (V) Luas permukaan (L) Luas alas (La) Luas selimut (Ls) Jari-jari (r) diketahui V Jari-jari (r) diketahui L Jari-jari (r) diketahui Ls Tinggi (t) diketahui V Artikel terkait: Contoh Soal Kerucut
-
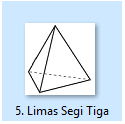
Limas Segitiga
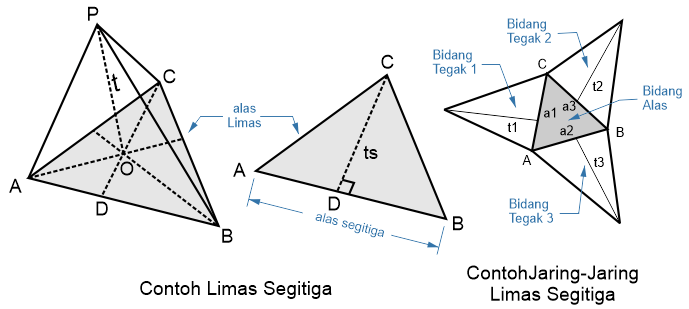
Limas segitiga adalah bangun ruang berjenis limas yang mempunyai sisi alas berbentuk segitiga. Secara umum, Limas adalah jenis bangun ruang yang mempunyai sisi alas berbentuk segi-n dan mengerucut ke satu titik sehingga terbentuk sisi-sisi tegak berbentuk segitiga.
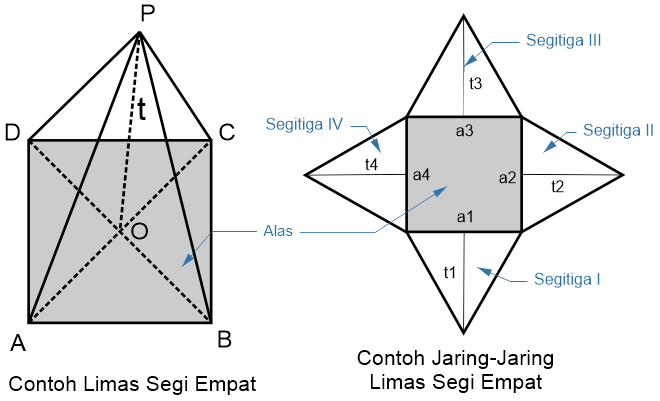
Keterangan: t = tinggi limas (PO) as = alas segitiga (AB) ts = tinggi segitiga alas (DC) t1, t2, t3 = tinggi masing-masing bidang tegak a1, a2, a3 = alas masing-masing bidang tegak
Artikel terkait: Contoh Soal Limas
-
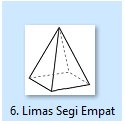
Limas Segiempat
Limas segi empat adalah bangun ruang sejenis limas yang mempunyai alas segi empat (persegi, persegi panjang, belah ketupat, layang-layang, jajar genjang atau trapesium).
Rumus Limas Segi Empat
Nama Rumus Volume (V) V = ⅓ × L alas × t Luas Permukaan (L) L = L alas + L ΔI + L ΔII + L ΔIII + L ΔIV Tinggi t = (3 × V) ÷ L alas Luas Alas Limas Segi Empat
Jenis Alas Luas Alas (La) Alas Persegi La = s × s Alas Persegi Panjang La = p × l Alas Jajar Genjang La = a × t Alas Trapesium Alas Belah Ketupat La = ½ × d1 × d2 Alas Layang-Layang La = ½ × d1 × d2 Luas Sisi Tegak Limas Segi Empat
Sisi Tegak Luas Luas ΔI L ΔI = ½ × a Δ1 × t Δ1 Luas ΔII L ΔII = ½ × a Δ2 × t Δ2 Luas ΔIII L ΔIII = ½ × a Δ3 × t Δ3 Luas ΔIV L ΔIII = ½ × a Δ4 × t Δ4 Artikel terkait: Contoh Soal Limas Segi Empat
-
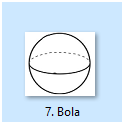
Bola
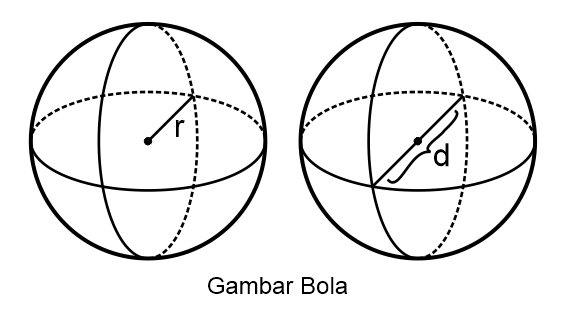
Bola adalah bangun ruang dengan bentuk bulat sempurna yang tersusun oleh tidak terhingga lingkaran yang mempunyai jari-jari dan pusat lingkaran yang sama.
jari-jari (r) = d÷2 diameter (d) = 2×r π = 22/7 untuk jari-jari kelipatan 7 dan 3,14 untuk jari-jari bukan kelipatan 7Nama Rumus Volume (V) V = 4/3 × π × r³ Luas Permukaan (L) L = 4 × π × r² Jari-jari (r) diketahui V Jari-jari (r) diketahui L Artikel terkait: Contoh Soal Bola
-
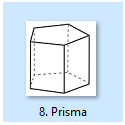
Prisma
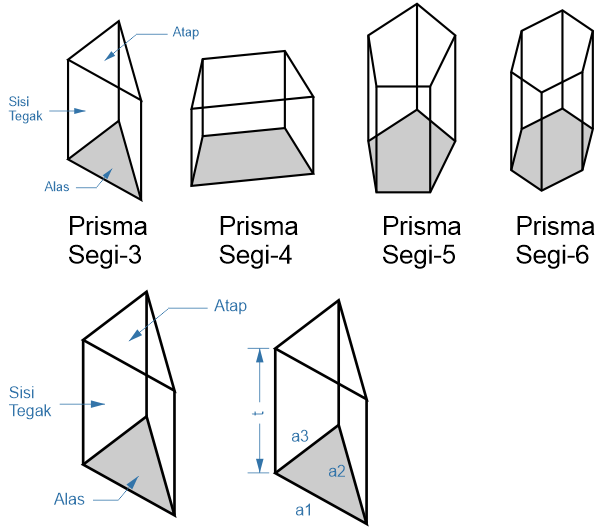
Prisma adalah bangun ruang yang terdiri dari atap dan alas dengan bentuk segi-n yang kongruen beserta dipisahkan oleh sisi-sisi tegak berbentuk segi empat.
t = tinggi prisma La = luas alas
Nama Rumus Volume (V) V = Luas alas × t tinggi (t) jika diketahui V t = V ÷ Luas Alas Luas Permukaan (L) L = t × ( a1 + a2 + ... + an) + (2 × La) L = t × (Keliling Alas) + (2 × La) ∴ Luas Prisma Segi-3 L = t × ( a1 + a2 + a3) + (2 × La) ∴ Luas Prisma Segi-4 L = t × ( a1 + a2 + a3 + a4) + (2 × La) ∴ Luas Prisma Segi-5 L = t × ( a1 + a2 + a3 + a4 + a5) + (2 × La) ∴ Luas Prisma Segi-6 L = t × ( a1 + a2 + a3 + a4 + a5 + a6) + (2 × La) Luas Alas (La) Disesuaikan dengan bentuk prisma Artikel terkait: Contoh Soal Prisma
Untuk contoh soal dan pembahasan untuk masing-masing bangun disediakan pada artikel terkait di bawah tabel rumus.
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel "8 Rumus Bangun Ruang | Pengertian, Gambar, Volume, Luas, dan Contoh Soal". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih...


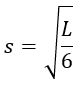
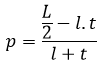
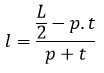
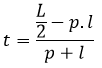
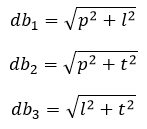
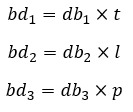
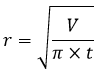
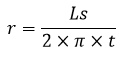
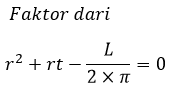
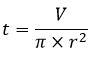
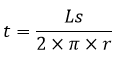
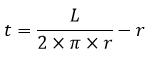
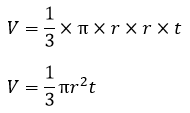
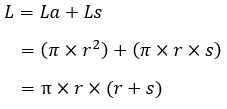
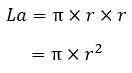
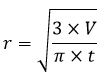
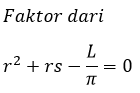
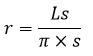
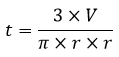
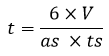
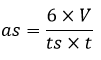
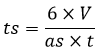
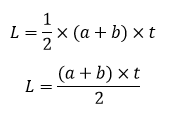
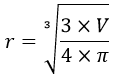
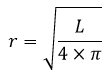










Wah, sangat jelas sekali penjelasannya 👏👏👏
Terima kasih, Azzrilazzam
Atas review-nya 🙂
wah ada ajam
MANTHAPPPPPPPPPPPPPP
Terima kasih Kak Zeus
Senang dapat membantu 🙂
wahh detail banget penjelasan nyaa , sangat membantuu
Gomawo advernesia ishga naleul deo ihaehage haejugi ttaemun-e jeongmal johseubnida. 🙂 _#GOMAWO#_
Terima kasih Kak Syavir
Atas review-nya 🙂
Wahhhh manteppp jelas sekali kaya poster
Terima kasih Kak Dimas
Senang dapat membantu 🙂
mantap ini mah, perlu dicatat
Terima kasih Kak Hareets
Senang dapat membantu proses belajarnya 🙂
Jelas banget,thank you kak..
Hai, Dik Vira
It's My pleasure 🙂
Makasih banyak Kakak Kakakku ♥️♥️♥️
Terima kasih kembali Vita Andriana
Senang dapat membantu proses belajar kamu 🙂
thank you sis, very helpful
Terima kasih kakak udah membantu. Saya jadi makin mengerti tentang rumus² matematika
Hai, Dik Azizah
Senang dapat membantu proses belajarnya 🙂
mantap kak thankyou
Terima kasih atas ulasannya Aland
Senang dapat membantu proses belajarnya 🙂
Jadi makin asik nih belajar matematika, terimakasih advernesia!
terima kasih Sekar 🙂
Wah terimakasih,aku terbantu sekalii..
Hai, Kak Hudalatiful
Senang dapat membantu pekerjaannya 🙂
Wah bagus nggak seperti lainnya yang ini lebih jelas
Hai, Kak Fatin
Sebagai pengelola saya senang mendengarnya
Advernesia akan terus meningkatkan kualitas artikel 🙂
Terima kasih kakak ini sangat membantu untuk aku hafalkan
Hai, Dik Zhilal
Senang dapat membantu proses belajarnya
Semoga dapat membantu untuk memahami lebih jelas 🙂
Makasih kak,disini ada semuany, lengkap,trus aku jg gampang hfalinnya,the best deh🥺👑
Hai, Lalala
Silakan juga akses contoh soalnya untuk latihan
Semoga dapat membantu untuk memahami lebih jelas 🙂
Keren, bagus lengkap lagi thankyou
Thanks juga Kak Maria
Senang membantu proses belajarnya 🙂
WAH DAEBAK...KAK PENJELASAN NYA JELAS SEKALI Gomawo kak
Wah, Saya sangat senang mendengarnya
Silakan membaca tutorial lainnya, Nabila 🙂
maaci, membantu banget
Hai, Dik Neo
Senang dapat membantu, semoga proses belajarnya menjadi lebih mudah 🙂
Iiih pas lihat disini rumus rumusnya aku jadi lebih paham
Hai, Dik Keysa
Saya sebagai pengelola sangat senang mendengarnya 🙂
Terima kasih kak udah memberitahu rumus dari luas dan volume bangun ruang, aku bersyukur banget jika punya kakak kayak anda😄
Hai, Alfin
Senang dapat membantu kamu dalam proses belajarnya 🙂
Wah mantap kak advernesia !!
Rumus nya benar semua, dan mudah
Menghapal nya
Hai, Alex
Sebagai pen pengelola saya sangat senang mendengarnya
Semoga mempermudah belajarnya 🙂