A. Pengertian Akar Pangkat 2 atau Akar Kuadrat (Square Root)
Akar kuadrat atau akar pangkat 2 adalah kebalikan dari operasi pangkat 2 atau invers pangkat 2 suatu bilangan. Nilai akar pangkat 2 suatu bilangan x adalah y dimana berlaku x = y², dengan x dan y bilangan real. Sehingga dapat ditulis √x = y dan dibaca "akar kuadrat dari x sama dengan y". Akar kuadrat dalam bahasa inggris disebut "square root".
Konsep Dasar
Untuk memahami konsep akar kuadrat, kita perlu memahami konsep perpangkatan khususnya perpangkatan 2.
Baca lebih lanjut: Perpangkatan dan Cara Menghitung Pangkat
Contoh: √144 = 12 Karena 12² = 12 × 12 = 144
Navigasi Cepat
- B. Cara Menghitung Akar Kuadrat
- Metode Ekstraksi
- Contoh: Menghitung √484, √625, dan √15.129
- C. Akar Kuadrat Tidak Sempurna
- Contoh: Menghitung √35
B. Cara Menghitung Akar Kuadrat (Ekstraksi)
Sebelum ditemukan kalkulator, menghitung akar kuadrat menjadi topik hangat di kalangan matematikawan untuk menemukan metode yang efektif dan efisien. Sehingga mencari akar pangkat 2 bukanlah hal sederhana secara keilmuan.
Metode Ekstraksi (Longhand Method)
Berdasarkan catatan J.B Calvert (1999), metode ekstraksi (longhand method) merupakan yang paling mudah untuk digunakan. Metode ini bekerja dengan memisahkan 2 digits bilangan yang dihitung. Selain itu, terdapat banyak metode lain untuk menghitung akar kuadrat seperti metode logaritma (tercepat) atau dengan metode aritmatika yang lebih akurat. Berikut dasar penggunaan metode ekstraksi,
-
Memahami Perpangkatan 2
Pangkat 2 Akar Pangkat 2 1² = 1 × 1 = 1 √1 = 1 2² = 2 × 2 = 4 √4 = 2 3² = 3 × 3 = 9 √9 = 3 4² = 4 × 4 = 16 √16 = 4 5² = 5 × 5 = 25 √25 = 5 6² = 6 × 6 = 36 √36 = 6 7² = 7 × 7 = 49 √49 = 7 8² = 8 × 8 = 64 √64 = 8 9² = 9 ×9 = 81 √81 = 9 10² = 10 ×10 = 100 √100 = 10 -
Mengekstrak Bilangan
Untuk mengekstrak bilangan dimulai 2 digits dari satuan.
11 1 11 11 11 1 11 11 11 11 11 11 11 11, 10 11 11 11, 11 11 11 11, 11 10 dan seterusnya
-
Mencari akar ekstraksi pertama dari kiri
-
Mencari akar ekstraksi selanjutnya
- Proses pengurangan
- Menurunkan ekstraksi selanjutnya
- Mencari pasangan perkalian dari 2x nilai akar ekstraksi
-
Melakukan langkah 4 hingga menemukan hasil terdekat
Contoh 1: Akar kuadrat dari 484
Penyelesaian:
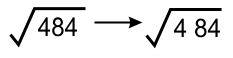
* Mengekstrak bilangan dari √484
Mengekstrak 2 digits bilangan dari satuan
* Mencari akar ekstraksi pertama dari kiri, yaitu 4
Akar terdekat atau tepat dari √4 adalah 2, karena 2² = 4 (Nilai diambil saat hasil paling mendekati dan tidak melebihi 4)
* Mengurangkan nilai kuadrat 2² = 4, lalu menurunkan ekstraksi berikutnya
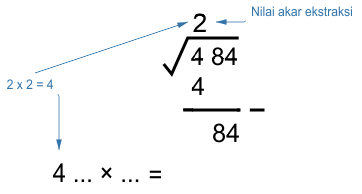
* Mencari pasangan perkalian dari "2x" nilai akar ekstraksi (2)
Nilai (...) adalah suatu bilangan bulat yang memenuhi 4 (...) × (...) ≅ 84
Catatan: ≅ merupakan tanda sama dengan atau hampir mendekati
UNTUK mencari perlu dicoba setiap bilangan bulat hingga mendekati ≅ 84
41 × 1 = 41 42 × 2 = 84 43 × 3 = 129 ...
Sehingga diperoleh nilai (...) = 2, KARENA 42 × 2 = 84.
* Karena hasil pengurangan ekstraksi telah habis, maka proses ekstraksi telah selesai.
Jadi, √484 = 22
Baca juga: Cara Menghitung Akar Pangkat 3
Contoh 2: Akar kuadrat dari 625
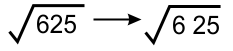
* Mengekstrak bilangan dari √625
Mengekstrak 2 digits bilangan dari satuan
* Mencari akar ekstraksi pertama dari kiri, yaitu 6
Yang paling mendekati √6 ≅ 2, karena 2² = 4 (Nilai diambil saat hasil paling mendekati dan tidak melebihi 6)
* Mengurangkan nilai kuadrat 2² = 4, lalu menurunkan ekstraksi berikutnya
* Mencari pasangan perkalian dari "2x" nilai akar ekstraksi (2)
Nilai (...) adalah suatu bilangan bulat yang memenuhi 4 (...) × (...) ≅ 225
Catatan: ≅ merupakan tanda sama dengan atau hampir mendekati
UNTUK mencari perlu dicoba setiap bilangan bulat hingga mendekati ≅ 225
... 43 × 3 = 129 44 × 4 = 176 45 × 5 = 225 46 × 6 = 276 ...
Sehingga diperoleh pasangan angka 5
* Karena hasil pengurangan ekstraksi telah habis, maka proses ekstraksi telah selesai.
Jadi, √625 = 25
Contoh 3: Akar kuadrat dari 15.129
* Mengekstrak bilangan dari √15.129
Mengekstrak 2 digits bilangan dari satuan
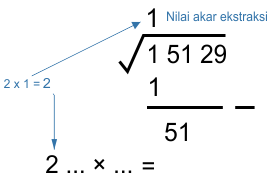
* Mencari akar ekstraksi pertama dari kiri, yaitu 1
Akar terdekat atau tepat dari √1 adalah 1, karena 1² = 1 (Nilai diambil saat hasil paling mendekati dan tidak melebihi 1)
* Mengurangkan nilai kuadrat 1² = 1, lalu menurunkan ekstraksi berikutnya
* Mencari pasangan perkalian dari "2x" nilai akar ekstraksi (1)
Nilai (...) adalah suatu bilangan bulat yang memenuhi 2 (...) × (...) ≅ 51
Catatan: ≅ merupakan tanda sama dengan atau hampir mendekati
UNTUK mencari perlu dicoba setiap bilangan bulat hingga mendekati ≅ 51
... 21 × 1 = 21 22 × 2 = 44 23 × 3 = 69 ...
Sehingga diperoleh pasangan angka 2 , karena pasangan 1 (21) lebih kecil (21) dari pasangan 2 (44) dan pasangan 3 (69) lebih besar namun melebihi 51.
* Mengurangkan dan menurunkan ekstraksi berikutnya (ekstraksi belum habis)
* Mencari pasangan perkalian dari "2x" nilai akar ekstraksi (12)
Nilai (...) adalah suatu bilangan bulat yang memenuhi 24 (...) × (...) ≅ 729
Catatan: ≅ merupakan tanda sama dengan atau hampir mendekati
UNTUK mencari perlu dicoba setiap bilangan bulat yang menghasilkan ≅ 729
241 × 1 = 241 242 × 2 = 484 243 × 3 = 729 ...
Sehingga diperoleh pasangan angka 3
* Karena hasil pengurangan ekstraksi telah habis, maka proses ekstraksi telah selesai.
Jadi, √15.129 = 123
C. Cara Menghitung Akar Kuadrat Tidak Sempurna
Akar tidak sempurna adalah nilai akar yang menghasilkan bilangan desimal atau tidak bulat. Saat menggunakan metode ekstraksi, akar tidak sempurna menghasilkan nilai bukan 0 saat semua ekstraksi bulat habis (di depan koma). Jadi untuk menghitungnya diambil ekstraksi desimal berikutnya, hingga hasil yang diperoleh dapat mendekati nilai akar tidak sempurna.
Contoh: Akar kuadrat dari 35
* Mengekstrak bilangan dari √35
Bilangan ini hanya terdiri dari 2 digits, jadi hasil ekstraksi tetap √35
* Mencari akar ekstraksi pertama dari kiri, yaitu 35
Akar terdekat dan tidak melebihi √35 adalah 5, karena 5² = 25 (Nilai diambil saat hasil paling mendekati dan tidak melebihi 35)
* Mengurangkan nilai kuadrat 5² = 25
* Ekstraksi bulat habis, namun pengurangan bersisa. Ambil ekstraksi desimal
* Mencari pasangan perkalian dari "2x" nilai akar ekstraksi (5)
Nilai (...) adalah 1 digit tambahan bilangan desimal yang memenuhi 10, (...) × (...) ≅ 10,00
Catatan: ≅ merupakan tanda sama dengan atau hampir mendekati
UNTUK mencari perlu dicoba setiap bilangan bulat hingga mendekati ≅ 10,00
10,1 × 0,1 = 1,01 10,2 × 0,2 = 2,04 ... 10,9 × 0,9 = 9,81
Jadi 1 digit nilai desimal yang paling mendekati adalah 0,9
Sampai proses ekstraksi desimal pertama sudah diperoleh hasil √35 ≈ 5,9
* Tidak puas dengan hasilnya, ulangi ke ekstraksi desimal berikutnya
Nilai (...) adalah 1 digit tambahan bilangan desimal yang memenuhi 11,8 (...) × (...) ≅ 0, 19 00
Catatan: ≅ merupakan tanda sama dengan atau hampir mendekati
UNTUK mencari perlu dicoba setiap bilangan bulat hingga mendekati ≅ 0, 19 00
11,81 × 0,01 = 0,1181 10,82 × 0,02 = 0,2164 ...
Jadi 1 digit nilai desimal yang paling mendekati adalah 0,01
Langkah di atas menghasilkan nilai yang lebih detail, langkah tersebut dapat dilanjutkan untuk menghasilkan nilai yang lebih detail lagi.
Jadi, √35 = 5,91 ...
Kontributor: Deardo (Pemeriksa)
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel “Akar Pangkat 2 | Cara Menghitung Akar Kuadrat dan Contohnya“. Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih…


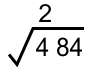
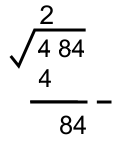
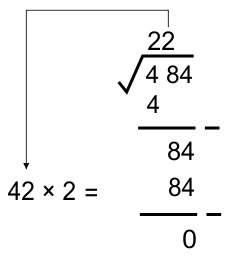
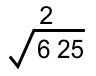
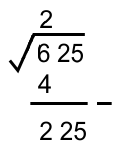
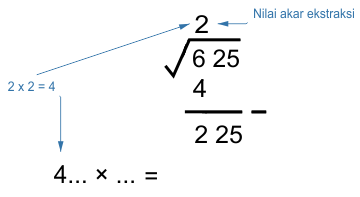
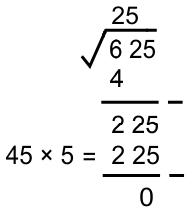

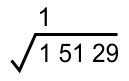
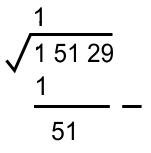
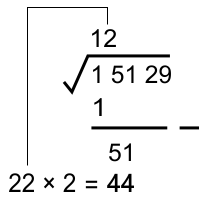
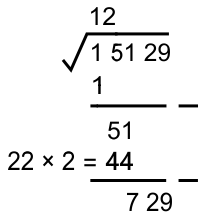

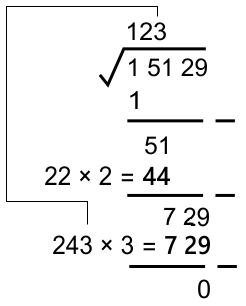
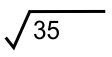
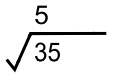
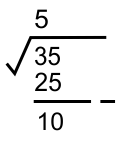
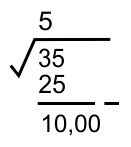
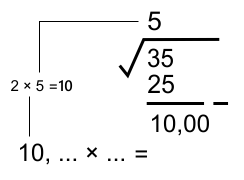
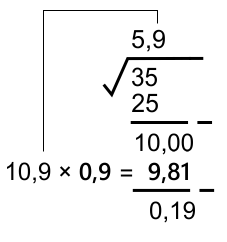
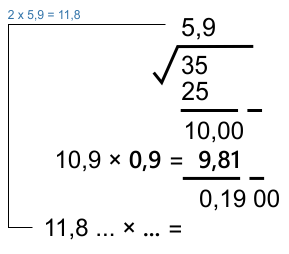
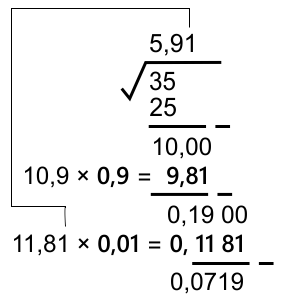













Thanks ya akak
You're welcome dik Rutija Lovery 🙂
√35 terakhir 1900 11,8 * 1,6 = 18,88
1900 - 1888 = 12 mentok
591*2=11,82
Mohon diperjelas singkat terimakasih 🙏
Bagian akhir itu ekstraksi desimal ke dua 0.1900 - (2 x 5.9[a]) x 0,0[a] dengan a yang memenuhi adalah 1 karena angka 2 menghasilkan nilai yang lebih tinggi dari 0.1900
0.1900 - (11.8[1] x 0.0[1]) = 0.1900 - 0.1181 = 0.0719
Jadi, hasil akar 35 di ekstraksi desimal kedua adalah 5,9[1]
Semoga memperjelas 🙂
Penjelasannya super sekali.hanya sekali baca aja aku langsung paham.dan aku jadi bisa ngajarin anak yg belum paham mengerjakan soal akar kuadrat dengan metode ekstraksi.makasih....makasih....makasih....🤗
Wah terima kasih kembali atas feedbacknya kak Nuning,
Saya sangat senang mendengarnya 🙂
Contoh yang 4 digitnya gaada ?
Hai kak rizalpradiptaarya,
Caranya sama saja, dengan mengekstraksi 2 digit dari satuan 1234 = 12 34
Semoga membantu 🙂
Kalau penyerderhaan √4.47
Hai Taufik, ekstraksi √4.47 dimulai dari satuan menjadi 4. 47
Semoga bermanfaat 🙂
makasih 🙂 ya kak -.<
Sama-sama Cherlina Aisyah atas apresiasinya 🙂
Izin bertanya ka kalo seandainya √64 penjabarannya seperti apa?
Hai Miftah, berikut penjabaran √64
Untuk akar kuadrat dari -100 hingga 100 dapat dilakukan tanpa melakukan penjabaran
Semoga membantu 🙂
Kalau misal 788 kak.. Bilangan pangkat 2 yang hasilnya 8 gak ada kak.. Ini gimana solusinya kak ?
Makasih ya kak 😆😆😆
Hai, Fitriani
Terima kasih kembali atas review-nya,
Senang dapat membantu 🙂
Sepertinya ada beberapa kesalahan saat mengalikan 2×1.. jawabanya 1.. harusnya kan 2..
Halo kak namaku putri salken ya kak😁😁
Hai, Putri salam kenal juga ya
Selamat datang di Advernesia
Semoga membantu proses belajar kamu ya 🙂
Kalau akar 4096 bagaimana ?
Terima kasih kak, ilmu nya bermanfaat banget
Hai, Dik Fauzan
Senang dapat membantu, semoga memperjelas tentang materi akar kuadrat 🙂
wahhh jdi lebih faham aku nih.maksh kaka😊
Hai, Eky Nurul Islami
Senang dapat membantu proses belajarnya 🙂
Mohon bantuan penyelesaian dari √6589489 dong kak
Hai, Kak Aini
√6 589 489 = √6 58 94 89
Sehingga diperoleh
2567 __________ /6 58 94 89 4 _____________ _ 2 58 45 x 5 = 2 25 _____________ _ 33 94 506 x 6 = 30 36 _____________ _ 3 58 89 5127 x 7 = 3 58 89 _____________ _ 0Semoga membantu 🙂
Makasih ka penjelasanya aku jadi ngerti , semoga ilmu nya bermanfaat buat orang banyak 🙏
Senang dapat membantu Aulia Nidda
Terima kasih atas ulasannya 🙂
Makasih ka penjelasannya, langsung ngerti
sama sama Gibran 🙂
Dapat 506 darimana kak?
Dapat 5127 juga dari mana?
Hai, Kak Enji itu proses (4) mencari akar ekstraksi selanjutnya
Semoga membantu 🙂
Terimakasih atas ilmunya. Semoga diberikan pahala yang berlipat 🙏🏻
Terima kasih Dik Anis, Amin ...