A. Pengertian Teorema Pythagoras
Teorema Pythagoras adalah pernyataan mengenai hubungan antara sisi-sisi sebuah segitiga siku-siku. Teorema Pythagoras ditemukan pada abad ke-6 SM oleh Pythagoras, seorang filsuf dari Yunani Kuno (Ancient Greek) yang dikenal dengan sebutan "Πυθαγόρας ὁ Σάμιος" yang berarti "Pythagóras o Sámios". Pythagoras hidup di zaman Yunani Kuno, lahir di Sámios sekitar tahun 570 SM hingga meninggal sekitar tahun 495 SM (tahun sebelum masehi dihitung mundur). Teorema Pythagoras menjadi konsep dasar pembentukan rumus Pythagoras di zaman yang lebih modern.
Simon Singh (1998) dalam bukunya menyatakan sebelum lahirnya Pythagoras, teorema tersebut telah ada. Pythagoras merupakan orang pertama yang membuktikan teorema ini secara matematis. Pythagoras dinobatkan sebagai penemu teorema tersebut dengan nama "Teorema Pythagoras". Selain itu Pythagoras juga berjasa terhadap teori bilangan, geometri, hingga ilmu filsafat. Pemikiran Pythagoras memberikan pengetahuan terhadap filsuf Yunani kuno terkenal berikutnya untuk menemukan atau menciptakan hal baru, misalnya Plato. Selanjutnya Pythagoras dikenal sebagai "Bapak Matematika" karena menjadi tokoh awal terhadap perkembangan ilmu matematika.
Navigasi Cepat:
- B. Rumus Pythagoras "Segitiga Siku-Siku"
- C. Rumus Pythagoras "Luas Persegi"
- D. Angka Triple Pythagoras
Terdapat 2 pernyataan dari teorema Pythagoras, yaitu pernyataan tentang segitiga siku-siku dan pernyataan tentang luas persegi pada sisi segitiga siku-siku. Hal ini menjadi konsep dasar untuk membuat rumus Pythagoras.
B. Rumus Pythagoras "Segitiga Siku-Siku"
Teorema Pythagoras menyatakan:
"Segitiga siku-siku adalah segitiga yang mempunyai sudut siku-siku, kakinya adalah 2 sisi yang membentuk sudut siku-siku, dan hipotenusa adalah sisi miring yang berhadapan dengan kakinya"
Artikel terkait: Jenis Segitiga, Rumus Luas dan Keliling Segitiga
Berikut rumus Pythagoras:
dengan: a,b = kaki segitiga; dan c = sisi miring (hipotenusa)
Contoh Soal 1: Menghitung Sisi Miring
Sebuah segitiga siku-siku mempunyai sisi datar 3 cm dan sisi tegak 4 cm. Hitunglah sisi miringnya!
Diketahui:
a = 3 cm, b = 4 cm
Ditanya:
Sisi miring (c)!
Penyelesaian:
Jadi, sisi miring segitiga siku-siku tersebut adalah 5 cm.
Contoh Soal 2: Menghitung Kaki Segitiga Siku-Siku
Diketahui sebuah segitiga siku-siku mempunyai sisi miring 10 cm dan sisi datar 8 cm. Tentukan sisi tegak segitiga siku-siku tersebut!
Diketahui:
c = 10 cm, a = 8 cm
Ditanya:
Sisi tegak segitiga siku-siku!
Penyelesaian:
Jadi, sisi tegak segitiga siku-siku adalah 6 cm.
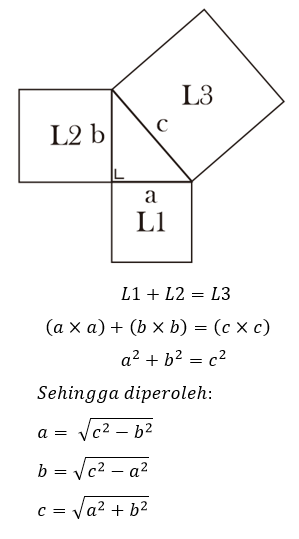
C. Rumus Pythagoras "Luas Persegi"
Teorema Pythagoras menyatakan:
"Pada segitiga siku-siku, jumlah luas persegi pada kakinya sama dengan luas persegi pada sisi miringnya (hipotenusa)"
D. Angka Triple Pythagoras (Pythagorean triple)
Angka triple Pythagoras adalah 3 angka bilangan asli yang memenuhi teorema Pythagoras, 3 angka ini merupakan panjang sisi segitiga siku-siku yang dibentuk.
Artikel terkait: Pengertian Bilangan Cacah dan Bilangan Asli Beserta Contohnya
Berikut merupakan angka triple Pythagoras primitif yang kurang dari 100. Angka triple Pythagoras primitif dapat menghasilkan angka triple Pythagoras non-primitif. Misalkan angka primitif 3, 4, 5 dapat membentuk angka (6, 8, 10); (12, 16, 20); dan seterusnya.
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (39, 80, 89) | (65, 72, 97) |
Misalnya (3, 4, 5) berarti sisi a = 3, b = 4, dan c = 5, akan membentuk segitiga siku-siku.
Singh, Simon (1998). Fermat's Enigma. New York: Anchor Books.
Baca juga: Daftar Isi Pelajaran Matematika
Sekian artikel "Rumus Pythagoras Segitiga dan Contoh Soalnya". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai Fans Page Advernesia. Terima kasih …


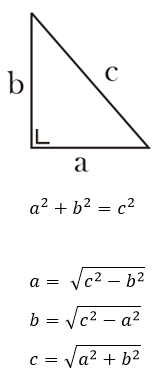
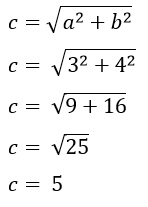
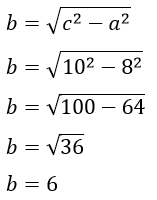













Terima kasih. Sangat membantu saya dalam belajar matematika.
Terima kasih kembali Lukman atas komentarnya 🙂
Bang/kak
tolong jelasin cara mengetahui rumus luas sgtiga sama kaki tanpa tinggi
Hai Moris No Limit,
rumus tinggi segitiga sama sisi = √(kaki² - (a/2)²)
Sebagai catatan, nilai kaki diambil satu saja.
Semoga membantu 🙂
😉😉😉😉 sangat membantu trimakasih
Terima kasih Kayla atas reviewnya
Senang dapat membantu 🙂
Sangat membantu sekali rumus2nya...😊
Semoga selalu semangat ya... 💪
Terima kasih Kak Agustin Fauziah
Telah memberikan semangat 😊😊😊
kak tolong kalo kek gini gmn ya di ketahui besar segitiga abc = 45derajat cad = 30 derajat nah cara mencari perbandingan sebuah segitiga gimana kak
Hai kak samuel,
Perbandingan apa yang dicari?
Jika sudut, seluruh sudutnya berjumlah 180 derajat
kak tolong dong gimana ini " limas persegi dengan luas alas 64 dm2 dan tinggi limas 3 dm . Luas permukaan limas adalah ...
dm2 ( dm pangkat 2 )
terima kasihh
Ka,kalo segitiga yang tidak memenuhi rumus phytagoras apa aja kak?🙏
Hai, Kak Edio
Rumus Pythagoras berlaku terhadap segitiga siku-siku
Untuk segitiga lainnya tidak berlaku, namun dapat dilakukan slice terhadap segitiga bukan siku-siku untuk melakukan analisis geometri
Semoga membantu 🙂