Perpangkatan | Cara Menghitung Pangkat, Sifat, dan Tabel Perpangkatan

Penulis

Pengertian Perpangkatan atau Eksponen

Perpangkatan adalah operasi matematika untuk perkalian berulang suatu bilangan sebanyak pangkatnya. Pangkat suatu bilangan adalah angka yang ditulis lebih kecil dan terletak agak ke atas. Berdasarkan semantik penulisan huruf disebut dengan superscript, contoh: 2², 3², 4³, dan lainnya. Dalam bahasa inggris, perpangkatan disebut dengan "power" atau "exponent". Berikut dijelaskan mengenai cara menghitung perpangkatan, sifat, tabel pangkat 2, 3, dan 4.

Navigasi Cepat

A. Cara Menghitung Pangkat
B. Sifat Perpangkatan
C. Tabel Perpangkatan 2, 3, dan 4

A. Cara Menghitung Pangkat

Secara matematis perpangkatan bilangan dapat dituliskan sebagai berikut,

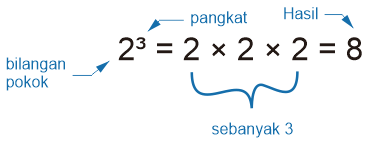
aⁿ = a × a × a × ... × a sebanyak n kali

a adalah bilangan yang dipangkatkan (bilangan pokok)
n adalah pangkat (eksponen)
dengan n adalah bilangan bulat positif

Contoh:
2³ = 2 × 2 × 2 = 8
Operasi di atas dibaca "dua pangkat tiga"

3⁴ = 3 × 3 × 3 × 3 = 81
Operasi di atas dibaca "tiga pangkat empat"

Catatan: Di tingkat yang lebih tinggi, nilai pangkat tidak hanya menggunakan bilangan bulat positif. Untuk menyelesaikannya diperlukan pemahaman mengenai sifat-sifat bilangan berpangkat lebih lanjut.

B. Sifat Perpangkatan

1. Semua Bilangan Pangkat 0 = 1

Berdasarkan konsep dasar, semua bilangan yang dipangkatkan 0 mempunyai hasil 1.

0⁰ = 1
1⁰ = 1
2⁰ = 1

Mengapa hal ini dapat terjadi?

Sebenarnya pembuktian ini memerlukan penjelasan teoritis yang lebih rumit, namun di sini akan dipaparkan secara sederhana dengan sifat pembagian bilangan berpangkat.

Misalnya 4⁰ = 1

4⁰ sama dengan operasi pembagian berikut:
Dengan mengambil sembarang pangkat bilangan bulat, misalnya 2

4⁰ =
= 4^2-2
= 4² : 4² 
= 16 : 16
= 1

2. Perkalian Bilangan Berpangkat

Jika p merupakan bilangan pokok, dan m, n merupakan pangkat. Dengan p, m, n merupakan bilangan real berlaku,

Catatan: Sifat khusus berikut berlaku pada operasi antar bilangan berpangkat apabila bilangan pokok masing-masing bernilai sama.

p^m × pⁿ = p^{m + n}
Contoh:
3² × 3⁴ = 3^{2 + 4} = 3⁶ = 729

Mengapa hal ini dapat terjadi?

Secara matematis, operasi bilangan berpangkat di atas dapat dituliskan

Secara matematis

3² × 3⁴ 
= (3 × 3) × (3 × 3 × 3 × 3)
= 3⁶
= 729

Perhitungan biasa menghasilkan hasil yang sama

3² × 3⁴ = 9 × 81 = 729

3. Pembagian Bilangan Berpangkat

Jika p merupakan bilangan pokok, dan m, n merupakan pangkat. Dengan p, m, n merupakan bilangan real berlaku,

Catatan: Sifat khusus berikut berlaku pada operasi antar bilangan berpangkat apabila bilangan pokok masing-masing bernilai sama.

p^m : pⁿ = p^{m - n}
Contoh:
3⁴ : 3² = 3^{4 - 2} = 3² = 9

Mengapa hal ini dapat terjadi?

Secara matematis

3⁴ : 3² 
= (3 × 3 × 3 × 3) : (3 × 3)
= (3 × 3)
= 9

Perhitungan biasa menghasilkan hasil yang sama

3⁴ × 3² = 81 : 9 = 9

4. Perpangkatan Bilangan Berpangkat

Jika p merupakan bilangan pokok, dan m, n merupakan pangkat. Dengan p, m, n merupakan bilangan real berlaku,

(p^m)ⁿ = p^{m × n}
Contoh:
(4²)³ = 4^{2 × 3} = 4⁶ = 4096

Mengapa hal ini dapat terjadi?

Secara matematis
(4²)³
= 4² × 4²× 4²
= 4^{2 + 2 + 2} 
= 4⁶
= 4096

Perhitungan biasa

(4²)³
= (16)³ 
= 4096

5. Bilangan dengan Pangkat Negatif

Secara matematis bilangan dengan pangkat negatif dapat dirumuskan sebagai berikut,

6. Bilangan dengan Pangkat Pecahan

Secara matematis bilangan dengan pangkat pecahan dapat dirumuskan sebagai berikut,

Untuk menyelesaikan bilangan dengan pangkat pecahan, perlu diketahui mengenai operasi akar bilangan.

Sekilas Operasi Akar

Operasi akar adalah kebalikan dari operasi perpangkatan atau dalam ilmu matematika disebut invers dari perpangkatan.

Baca selengkapnya: Cara Menghitung Akar Pangkat 2

Contoh: Akar pangkat 2
√144 = 12
Karena 12² = 12 × 12 = 144 

Contoh: Akar pangkat 3
³√1000 = 10
Karena 10³ = 10 × 10 × 10 = 1000

7. Perpangkatan Bilangan Pokok Negatif

Jika bilangan pokok negatif (-p) mempunyai pangkat m ganjil maka hasilnya negatif. Begitu juga sebaliknya, jika bilangan pokok negatif (-p) mempunyai pangkat m genap maka hasilnya positif. Dengan p dan m adalah bilangan real.

Saat m ganjil, (-p)^m = negatif
Saat m genap,  (-p)^m = positif

Contoh:

(-2)³ = (-2) × (-2) × (-2)
      = 4 × (-2) = -8

(-2)⁴ = (-2) × (-2) × (-2) × (-2)
      = 4 × (-2) × (-2)
      = (-8) × (-2)
      = 16

8. Perpangkatan Bilangan Pokok Non-Negatif Berbentuk Negatif

Bentuk perpangkatan untuk bilangan pokok non-negatif dapat memuat simbol minus di depan bilangan pokok tersebut. Tanda minus tersebut berfungsi sebagai pengali -1 terhadap bentuk perpangkatan tersebut. Bilangan pokok negatif perlu dipertegas dalam tanda kurung, karena pangkat mempunyai kedudukan yang lebih tinggi dari operasi perkalian dalam konsep dasar aritmatika, berikut ilustrasinya.

# Bilangan pokok negatif 
(-b)² = (-b) × (-b)

# Bilangan pokok non-negatif berbentuk negatif
  -b² = -1 × b²
      = -1 × b × b 

Contoh 8.1: Perbedaan (-3)² dan -3²

(-3)² = (-3) × (-3) = 9

∴ Terlihat bilangan pokok bentuk pangkat tersebut adalah negatif

-3² = -1 × 3²
    = -1 × 3 × 3 
    = -9

∴ Terlihat bilangan pokok bentuk pangkat tersebut adalah positif (non-negatif), nilai minus berfungsi sebagai pengali -1.

Contoh 8.2: Berapakah nilai dari -0⁰

-0⁰ = -1 × 0⁰
    = -1 x 1 = -1

∴ Terlihat bilangan pokok dari perpangkatan tersebut adalah nol (non-negatif).

C. Tabel Perpangkatan 2, 3, dan 4

Pangkat 2	Pangkat 3	Pangkat 4
1² = 1	1³ = 1	1⁴ = 1
2² = 4	2³ = 8	2⁴ = 16
3² = 9	3³ = 27	3⁴ = 81
4² = 16	4³ = 64	4⁴ = 256
5² = 25	5³ = 125	5⁴ = 625
6² = 36	6³ = 216	6⁴ = 1296
7² = 49	7³ = 343	7⁴ = 2401
8² = 64	8³ = 512	8⁴ = 4096
9² = 81	9³ = 729	9⁴ = 6561
10² = 100	10³ = 1000	10⁴ = 10000

Tutorial lainnya: Daftar Isi Pelajaran Matematika

Sekian artikel "Perpangkatan | Cara Menghitung Pangkat, Sifat, dan Tabel Perpangkatan". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih…

96 DISKUSI PEMBACA

Nia 25 Juli 2020 at 8:04 pm

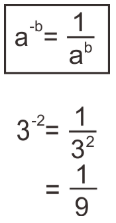
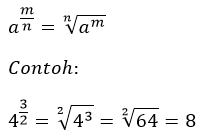
saya sudah memenuhi persyaratan nya

Balas
- Advernesia 25 Juli 2020 at 8:07 pm
  
  Hai, Nia, kalo boleh tahu, persyaratan apa ya?
  Semoga artikel ini bermanfaat ya 🙂
Roblox 28 Juli 2020 at 1:39 pm

1/2(6³-4²)=

Balas
- Advernesia 28 Juli 2020 at 4:39 pm
  
  Hai kak Roblok
  1/2(6³-4²) = 1/2 (216 - 16) = 1/2 (200) = 100
  Semoga membantu 🙂
Nadiva 1 Agustus 2020 at 1:50 pm

Hai Advernesia,,saya mau tanya hasil dari a pangkat 4

Balas
- Advernesia 1 Agustus 2020 at 1:53 pm
  
  Hai Navida, a dalam matematika umumnya berupa variabel, dan nilainya berubah-ubah sesuai dengan definisi variabel a ditentukan soal.
  Jadi a pangkat 4 = a x a x a x a, misalnya a = 3, maka a pangkat 4 = 3 x 3 x 3 x 3 = 81
  Semoga membantu 🙂
Jenny 3 Agustus 2020 at 11:21 am

Hai advernesia saya mau tanya hasil dari (-2)3 (-3)4 -34 -24 (-5a)4 (-2a) 70 -80 (-8)0 52 104 63 (3a)-3 3a-2

Balas
- Advernesia 3 Agustus 2020 at 11:29 am
  
  Hai Jenny, mohon ditulis tanda operasi hitungnya, juga
  Saya dapat mencoba membantu menghitungnya 🙂
- Pinklover 19 Oktober 2020 at 8:57 pm
  
  Kak gimana cara menyederhanakan 2/(×+3)-3/(×-2) tolong dibantu secepatnya ya kak
Khoirul 4 Agustus 2020 at 10:34 am

Hai Advernesia, hasil dari 1
—
x-³

Balas
- Advernesia 4 Agustus 2020 at 10:39 am
  Hai, Khoirul
```
 1     
---  = x³
x-³
```
  Ini bersesuaian dengan sifat pangkat negatif
  Semoga membantu 🙂
Ranti 4 Agustus 2020 at 7:59 pm

Hai advernesia, hasil dari (27)⅔

Balas
- Advernesia 4 Agustus 2020 at 8:10 pm
  Hai Ranti, hasilnya
```
(27)^²/₃ = ³√(27²)
= ³√(27 x 27)
= ³√(729)
= 9
Karena 9³ = 9 x 9 x 9 = 729
```
  Oh iya, Advernesia juga sudah membuat kalkulator online
  Bisa dicoba, semoga membantu ya 🙂
Aulia Ramadhani 7 Agustus 2020 at 9:10 pm

Hai, Advernesia! 🙂
Berapa bentuk sederhana dari 4^16×2^3:32^5 ?

Balas
- Advernesia 10 Agustus 2020 at 9:06 pm
  Hai Aulia Ramadhani
```
4¹⁶×2³:32⁵
ubah ke bilangan pokok 2
=2^{2^16}×2³:2^{5^5}
=2^{2 x 16} x 2³ : 2^{5 x 5}
=2³² x 2³ : 2²⁵
=2^{32 + 3 - 25}
=2¹⁰
= 1024
```
  Mohon maaf atas keterlambatan balasannya
  Semoga membantu 🙂
Christopher.Abby 8 Agustus 2020 at 10:39 am

No one is so rich that they can not help others, and no one is too poor to help others in some way

Balas
- Advernesia 10 Agustus 2020 at 11:53 pm
  
  Such a great quote Christopher Abby 🙂
Vika 8 Agustus 2020 at 10:59 am

Hai advernesia, hasil dari
1/m-3

Balas
- Advernesia 10 Agustus 2020 at 11:54 pm
  Hai Vika
```
 1     
---  = m³
m-³
```
  Semoga membantu 🙂
Opick 8 Agustus 2020 at 10:48 pm

3M pangkat 3 ×(MN)Pangkat 4

Balas
- Advernesia 10 Agustus 2020 at 11:51 pm
  Hai Opick
```
3M³ x (MN)⁴
=3M³ x M⁴N⁴
=3M³⁺⁴N⁴
=3M⁷N⁴
```
  Semoga membantu 🙂
lamkA 9 Agustus 2020 at 3:01 pm

Hai advernesia, sederhanakan (a³ x b^4 x c^6) x (a x b³ x c^2)^2

Balas
- Advernesia 12 Agustus 2020 at 7:38 am
  Hai Lamka
```
(a³ x b⁴ x c⁶) x (a x b³ x c²)²
= a³ x b⁴ x c⁶ x (a^1x2 x b^3x2 x c^2x2)
= a³ x b⁴ x c⁶ x (a² x b⁶ x c⁴)
= a³⁺² x b⁴⁺⁶ x c⁶⁺⁴ 
= a⁵ x b¹⁰ x c¹⁰
```
  maaf atas balasannya yang lambat, semoga membantu 🙂
Icha Nabila 10 Agustus 2020 at 8:50 pm

Hai advernesia, nilai hasil (64 pangkat 2/3) pangkat -3/4

Balas
- Advernesia 12 Agustus 2020 at 7:53 am
  Hai Icha Nabila
```
(64^2/3)^3/4
= 64^{2/3 x 3/4}
= 64^6/12
= 64²
= 4096
```
  Semoga membantu 🙂
- arykresna 10 Januari 2021 at 1:34 pm
  
  halo kak admin advernesia,
  kalo dari penyelesaian saya utk soal ini apakah benar :
  = 64^^6/12
  = 64^^1/2
  =²√64
  =8
  mohon koreksinya.
  terima kasih
- Advernesia 11 Januari 2021 at 1:34 pm
  
  Hai, Arya Kresna
  Iya penyelesaiannya benar
  Semoga membantu 🙂
Salwa 11 Agustus 2020 at 10:41 am

Hai Advernesia, hasil dari (3a) pangkat negatif 3

Balas
- Advernesia 12 Agustus 2020 at 8:08 am
  Hai Salwa
```
(3a)^-3
=3^-3a^-3
   1
= --- a^-3
   3³
= 1/27 a^-3
= 0.037a^-3 
```
  Semoga membantu 🙂
Airlangga 28 Agustus 2020 at 7:16 am

Hi adversia
Bagus materinya sangat membantu dan sangat jelas. Suka.

Balas
- Advernesia 28 Agustus 2020 at 10:13 pm
  
  Terima kasih Airlangga atas reviewnya
  Senang dapat membantu 🙂
Mhk737 7 September 2020 at 7:43 am

Nice n helpful

Balas
- Advernesia 7 September 2020 at 7:58 am
  
  Hai kak MosesHK, terima kasih atas review-nya
  Senang dapat membantu 🙂
Anggi 12 September 2020 at 10:11 am

8 pangkat ⅔ x 25 pangkat ½

Balas
- Advernesia 12 September 2020 at 10:21 am
  Hai Anggi
```
8^2/3 x 25^1/2
= ³√(8²) x ²√25
= ³√64 x 5
= 4 x 5
= 20
```
  Semoga membantu 🙂
Yuliarni 12 September 2020 at 11:45 pm

Bantu dong
Berapa 2,7 pangkat 0,485 ?

Balas
- Advernesia 13 September 2020 at 11:23 pm
  
  Hai kak Yuliarni
  Hasilnya 1.618867951998
  Semoga membantu 🙂
Sinta cahaya lestari 14 September 2020 at 10:18 am

Mohon bantuannya kak
2pngkat -3 + ⅛ =

Sekalian caranya ya, makasii.

Balas
- Advernesia 15 September 2020 at 9:54 pm
  Hai, Sinta Cahaya Lestari
```
2^-3 + 1/8 
= ¹/_2³ + 1/8
= 1/8 + 1/8
= 2/8
= 1/4
```
  Semoga membantu 🙂
Nci 15 September 2020 at 11:53 am

Bantu dong
Pangkat 2 log 6 × pangkat 6 log 12 × pangkat 12 log 8=....

Balas
- Advernesia 15 September 2020 at 10:20 pm
  Hai Nci, ini materi yang lebih tinggi dari perpangkatan
  Berdasarkan sifat logaritma
```
^alogb × ^blogc = ^alogc
```
  diperoleh
```
²log6 × ⁶log12 × ¹²log8
=²log12 × ¹²log8
=²log8
=3
Karena 2³=8
```
  Semoga membantu 🙂
Bayu 20 September 2020 at 7:08 pm

hai Advernesia Apa Ya Hasil Dari 6^3 X 2^4 Terimakasih

Balas
- Advernesia 21 September 2020 at 12:17 am
  Hai, Bayu
```
6³ × 2⁴
= (6 × 6 × 6) × (2 × 2 × 2 × 2)
= 216 × 16
= 232
```
  Semoga membantu 🙂