A. Pengertian Akar Pangkat 3 atau Cubic Root
Akar pangkat 3 adalah kebalikan dari perpangkatan 3 atau invers dari perpangkatan 3. Nilai akar pangkat tiga suatu bilangan x adalah y dimana berlaku x = y³, dengan x dan y bilangan real. Sehingga dapat ditulis ³√x = y dan dibaca "akar pangkat tiga dari x sama dengan y". Dalam bahasa inggris, akar pangkat tiga disebut dengan "cubic root".
Konsep Dasar
Untuk mempermudah memahami akar pangkat tiga, kita sebaiknya memahami materi perpangkatan dan akar pangkat 2.
Baca juga: Cara Menghitung Akar Pangkat 2
Contoh: Akar pangkat 3 dari 1728 ³√1728 = 1728 Karena 12³ = 12 × 12 × 12 = 1728
Navigasi Cepat
- B. Cara Menghitung Akar Pangkat 3
- Metode Ekstraksi
- Contoh: Menghitung ³√3.375 dan ³√1.771.561
- C. Akar Pangkat Tiga Tidak Sempurna
- Contoh: Menghitung ³√12
B. Cara Menghitung Akar Pangkat 3
Terdapat beberapa metode yang dapat digunakan untuk menghitung akar pangkat 3. Profesor J.B.Calvert dari University of Denver (1999) menyebutkan metode ekstraksi (longhand method) merupakan salah satu metode yang dapat digunakan untuk menyelesaikan akar pangkat tiga. Metode ini bekerja dengan memisahkan bilangan ke 3 digit dari satuan.
Metode Ekstraksi Akar Pangkat Tiga (Longhand Method)
Berikut langkah-langkah menghitung akar pangkat tiga dengan metode ekstraksi,
-
Memahami perpangkatan 3
Pangkat 3 Akar Pangkat 3 1³ = 1 × 1 × 1 = 1 ³√1 = 1 2³ = 2 × 2 × 2 = 8 ³√8 = 2 3³ = 3 × 3 × 3 = 27 ³√27 = 3 4³ = 4 × 4 × 4 = 64 ³√64 = 4 5³ = 5 × 5 × 5 = 125 ³√125 = 5 6³ = 6 × 6 × 6 = 216 ³√216 = 6 7³ = 7 × 7 × 7 = 343 ³√343 = 7 8³ = 8 × 8 × 8 = 512 ³√512 = 8 9³ = 9 × 9 × 9 = 729 ³√729 = 9 10³ = 10 × 10 × 10 = 1000 ³√1000 = 10 -
Mengekstrak bilangan
Untuk mengekstrak bilangan dimulai 3 digits dari satuan.
1 11 111 1 111 11 111 111 111 1 111 111 11 111 111 111 111 111, 100 dan seterusnya
-
Mencari akar pangkat tiga ekstraksi pertama
-
Mencari akar ekstraksi selanjutnya
-
Melakukan langkah 4 hingga menemukan hasil terdekat
Contoh 1: Akar Pangkat 3 dari 3375
Penyelesaian:
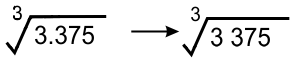
* Mengekstrak bilangan 3375
Langkah ini memisahkan bilangan menjadi 3 digits dari satuan.
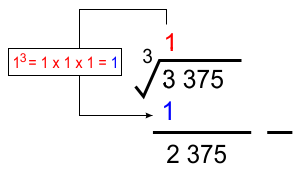
* Mencari akar bulat ekstraksi pertama (3)
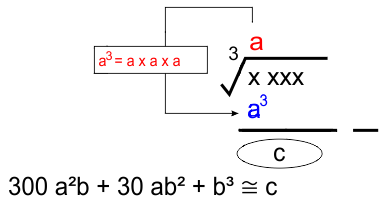
Ekstraksi pertama diambil dari kiri yaitu (3), sehingga ³√3 ≅ 1 (karena 1³ = 1, nilai harus bilangan bulat yang jika dipangkatkan 3 hasilnya paling mendekati dan tidak melebihi 3) (*dapat dilihat pada tabel perpangkatan 3)
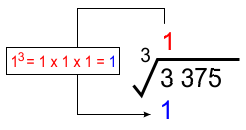
* Mengurangi bilangan dengan nilai akar ekstraksi (1) pangkat 3
* Menulis hasil pengurangan dan menurunkan ekstraksi berikutnya
* Menyelesaikan pasangan angka pada persamaan newton ≅ 2375
Untuk mencari pasangan angka, dapat dilakukan dengan mencoba angka yang dianggap mendekati hasil pengurangan terakhir ≅ 2375.
300 a²b + 30 ab² + b³ ≅ 2375 dengan a = 1
300 1²b + 30 1b² + b³ ≅ 2375
Dapat dicoba nilai b yang sekiranya mendekati 2375, misalnya b = 1, 2, 3, 4, 5, 6, dst hingga ditemukan hasil terdekat.
... (perhitungan b = 1, 2, 3 disembunyikan karena bukan terdekat)
300 (1)²(4) + 30 (1)(4)² + (4)³ ≅ 2375
1200 + 480 + 64 = 1744 ≅ 2375 (mendekati, sehingga perlu dicoba angka berikutnya)
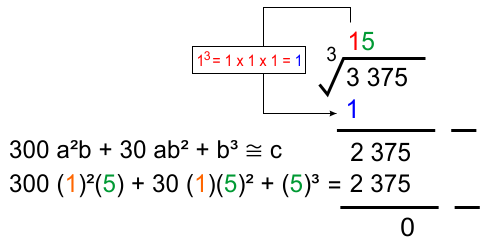
300 (1)²(5) + 30 (1)(5)² + (5)³ ≅ 2375
1500 + 750 + 125 = 2375 (tepat atau paling mendekati)
300 (1)²(6) + 30 (1)(6)² + (6)³ ≅ 2375
1800 + 1080 + 216 = 3096 (melebihi 2375, sehingga hasil tidak dapat diterima)
... (perhitungan dipotong, karena b = 6 melebihi nilai)
Sehingga akar ekstraksi selanjutnya adalah 5
* Semua ekstraksi telah diturunkan dan hasil akhir 0 (akar pangkat tiga sempurna), berarti perhitungan selesai
Hasil akhir 0 menunjukkan ³√3.375 adalah akar pangkat tiga sempurna karena hasilnya bilangan bulat (15).
Jadi, ³√3.375 = 15
Contoh 2: Akar pangkat 3 dari 1.771.561
Penyelesaian:
Dari angka ³√ 1.771.561 dapat diekstraksi menjadi ³√ 1 771 561, karena ekstraksi cukup banyak sehingga proses pencarian pasangan pada persamaan newton akan berulang hingga semua ekstraksi habis. Dengan mengikuti langkah pada contoh sebelumnya dapat dihitung:
* Ekstraksi pertama dan kedua
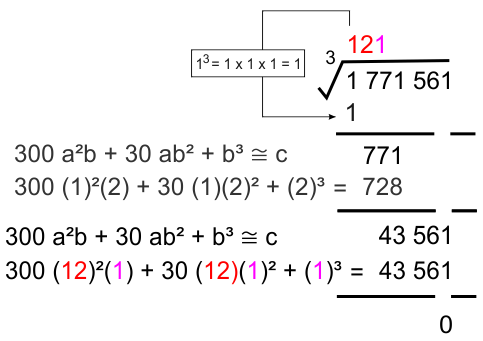
* Ekstraksi ketiga
* Semua ekstraksi telah diturunkan dan hasil akhir 0 (akar pangkat tiga sempurna), berarti perhitungan selesai
Hasil akhir 0 menunjukkan ³√1.771.561 adalah akar pangkat tiga sempurna karena hasilnya bilangan bulat (121).
Jadi, ³√1.771.561 = 121
C. Akar Pangkat 3 Tidak Sempurna
Akar pangkat tiga tidak sempurna menghasilkan nilai tidak bulat atau desimal. Saat menggunakan metode ini, setelah semua ekstraksi bulat habis, pengurangan tidak menghasilkan nilai 0. Sehingga diambil ekstraksi desimal untuk melakukan perhitungan selanjutnya hingga diperoleh hasil yang diharapkan.
Contoh: Akar pangkat 3 dari 12
Penyelesaian:
³√12 hanya terdiri dari 2 digits, sehingga ekstraksi tetap menghasilkan ³√12, dengan melakukan langkah seperti contoh sebelumnya dapat dihitung:
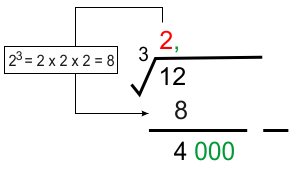
* Ekstraksi pertama
Dapat diperhatikan, ekstraksi telah habis, namun hasil pengurangan tidak 0. Sehingga ambil ekstraksi (3 digits) desimal dan tambahkan koma pada akar ekstraksi yang telah diperoleh.
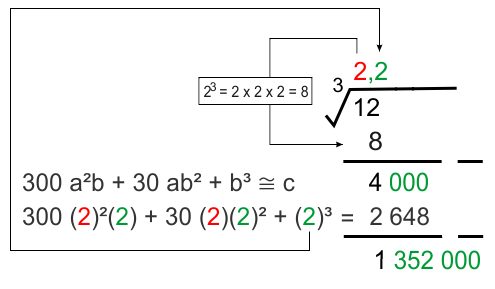
* Ekstraksi kedua (desimal)
Dengan mencoba angka bulat yang memenuhi persamaan newton diperoleh nilai b = 2, kemudian tulis di belakang koma nilai akar ekstraksi. Seperti gambar di atas.
Disini sudah diketahui ³√12 ≈ 2,2
Untuk mencari hasil yang lebih detail, dapat dilanjutkan dengan menghitung ekstraksi desimal berikutnya.
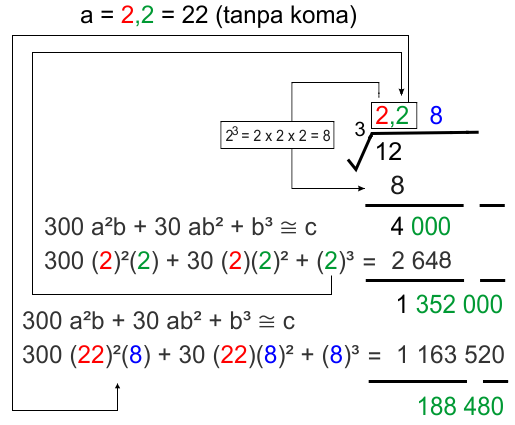
* Ekstraksi ketiga (desimal)
Catatan: pada persamaan newton tanda koma pada nilai a dihilangkan.
Langkah ini masih dapat dilanjutkan untuk menghasilkan nilai yang lebih detail lagi.
Jadi, ³√12 = 2,28 ...
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel “Akar Pangkat Tiga | Cara Menghitung Akar Pangkat Tiga“. Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih…


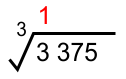
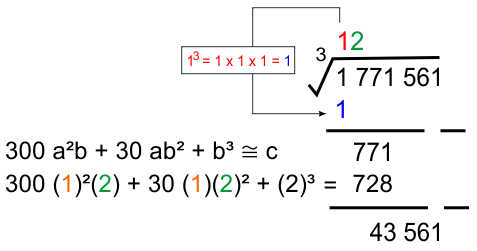













Terima kasih atas pengetahuannya
Terima kasih kembali kak Nanda,
Semoga membantu proses belajarnya 🙂
makasih yaa udah ngebantu aku belajar, doain dapet nilai bagus yaa
Terima kasih kembali atas apresiasinya Risyabelle
Semoga mendapat nilai bagus ya 🙂
naise bangett akhirnyaa tugas kapita selekta matematika dasar gua kelar :v
Hai Kak Sigit Pratama
Terima kasih atas feedback-nya 🙂
Trimakasih
Semoga bisa membantu
Terima Kasih Kak Ema Naifah Candra Ashilah atas reviewnya 🙂
Terima Kasih jawabannya.
Semoga daya dapat nilai seratus.
Hai, Dik Masayu Ismarini
Senang dapat membantu belajarnya, semoga dapat nilai seratus 🙂
kak 300 a² + 30 ab² + b³ ≅ c 300 itu nilai dari mana ya ?
apakah jika soalnya akar pangkat 4, ganti jadi 400 atau gmn ya kak ?
Hai, Kak Alen
Itu menggunakan teorema Binomial Newton
Untuk akar pangkat 4 berbeda lagi proses penyelesaiannya
Semoga membantu 🙂
terimakasih atas pelajarannya
Terima kasih atas ulasannya Fadhil
Advernesia terus menciptakan artikel-artikel yang mempermudah proses pembelajaran 🙂
mau tanya kak 0,11 √1600 hasilnya brp ya?
jawabannya 4.4, Diandri 🙂
saya suka sekali kk
iya dhena 🙂
maaf k maksud saya bagus sekali pelajaran matemaatika
kirain apa dhena ....
Terima kasih ya atas pelajarannya
Sama-sama Kak Grototo
Senang dapat membantu belajar matematika 🙂
Wah terimakasi banget ini sangat membantu saya latihan Pat
Doakan semoga nilai saya bagus😊