A. Pengertian Bilangan Prima
Bilangan prima adalah bilangan asli yang bernilai lebih dari 1 dan mempunyai 2 faktor pembagi yaitu 1 dan bilangan itu sendiri. Bilangan prima memiliki 2 faktor, berarti bilangan itu hanya habis dibagi oleh angka 1 dan bilangan itu sendiri. Kebalikan bilangan prima disebut dengan bilangan komposit.
Contoh: 2 adalah bilangan prima, karena angka 2 hanya bisa dibagi oleh angka 1 dan 2
Navigasi Cepat
- A. Pengertian Bilangan Prima
- B. Kebalikan Bilangan Prima (Komposit)
- C. Faktorisasi Prima dan Pohon Faktor
- D. Rumus Bilangan Prima (Cara Menentukan)
- E. Kegunaan Bilangan Prima
- F. Contoh Soal Bilangan Prima
Artikel terkait: Pengertian Bilangan Asli Beserta Contohnya
A1. Contoh bilangan Prima 1-100
Terdapat 25 bilangan prima antara 1-100
| 2 | 3 | 5 | 7 | 11 |
| 13 | 17 | 19 | 23 | 29 |
| 31 | 37 | 41 | 43 | 47 |
| 53 | 59 | 61 | 67 | 71 |
| 73 | 79 | 83 | 89 | 97 |
Angka 2 adalah satu-satunya bilangan prima genap.
A2. Contoh Bilangan Prima 1-1000
Terdapat 168 bilangan prima di antara angka 1-1000
1 bukanlah bilangan prima karena 1 hanya memiliki 1 faktor, sehingga bilangan prima dimulai dari angka 2.
2 merupakan satu-satunya angka prima genap, tidak terdapat bilangan prima lainnya yang bernilai genap.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997
A3. Tahukah Kamu: "Tidak ada bilangan prima terbesar"
Untuk setiap bilangan prima p, terdapat bilangan prima p 'seperti p' lebih besar dari p.
Bukti matematis ini ditunjukkan pada zaman kuno oleh matematikawan Yunani Euclid, ia melakukan validasi bahwa "tidak ada bilangan prima terbesar".
Berapakah bilangan prima terbesar yang telah ditemukan?
Nilai bilangan prima terbesar terus dicari secara formal oleh organisasi internasional yang bernama GIMPS (Great Internet Mersenne Prime Search). Bahkan organisasi ini menghadiahkan US$3000 untuk peneliti yang dapat menemukan bilangan prima terbesar selanjutnya yang menyentuh 100 juta digit angka. Berdasarkan catatan: Tahun 2019, bilangan prima terbesar adalah 282,589,933 − 1
B. Bilangan Komposit | Kebalikan Bilangan Prima
Kebalikan dari bilangan prima adalah bilangan komposit, yaitu bilangan asli bernilai lebih dari 1 serta memiliki lebih dari 2 faktor pembagi. Bilangan komposit, yaitu: 4, 6, 8, dan seterusnya.
Catatan: Angka Negatif, 0, dan 1 bukan termasuk bilangan komposit dan juga bukan bilangan prima. Hal ini disebabkan karena:
- Angka Negatif, karena bukan bilangan asli
- Angka 0, karena mempunyai tak terhingga faktor dan bukan bilangan asli
- Angka 1, karena hanya mempunyai 1 faktor
Artikel terkait: Pengertian Bilangan Komposit beserta Contohnya
C. Pengertian Faktorisasi Prima dan Pohon Faktor
Faktorisasi prima adalah bilangan-bilangan prima penyusun suatu bilangan komposit. Untuk mencari faktorisasi prima suatu bilangan dapat menggunakan bantuan pohon faktor.
Cara mencari faktorisasi prima suatu bilangan menggunakan pohon faktor adalah dengan membagi bilangan secara terus menerus dengan bilangan prima terkecil yang mungkin.
Contoh:
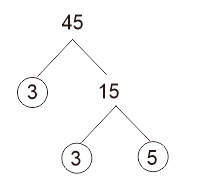
Carilah faktor prima dari 45?
Jadi, faktorisasi prima dari 45 adalah 3 × 3 × 5
Baca juga: Cara Mencari FPB (Faktor Persekutuan Besar) Berdasarkan Konsep Bilangan Prima (Pohon Faktor)
D. Rumus Bilangan Prima (Cara Menentukan Bilangan Prima)
Untuk mencari bilangan prima, harus ditentukan setiap bilangan yang dicari merupakan bilangan prima atau bukan. Berikut rumus untuk menentukan bilangan prima.
-
Tidak pernah berakhiran 0 dan 5, kecuali angka 5
Bilangan prima yang tersusun dari 2 angka atau lebih, tidak pernah berakhiran dengan satuan 0 dan 5.
Contoh: 10, 15, 20, 25, 30, 100, 12345, bukan bilangan prima.
-
Jumlah semua digit angka tidak pernah kelipatan 3
Angka yang terdiri lebih dari 2 digit atau lebih, apabila setiap digit dijumlahkan menghasilkan bilangan kelipatan 3. Maka angka tersebut akan habis dibagi 3 dan bukan merupakan bilangan prima.
Contoh: Angka 621, karena 6 + 2 + 1 = 9 (kelipatan 3), maka 621 habis dibagi 3, yaitu 621:3=207 (bukan prima, karena terbukti punya lebih dari 2 faktor). Angka 21117, karena 2 + 1 + 1 + 1 + 7 = 12 (kelipatan 3), maka habis dibagi 3, yaitu 21117:3=7039 (bukan prima, karena terbukti punya lebih dari 2 faktor).
-
Angka negatif, 0, dan 1 bukanlah bilangan Prima
-
Pohon faktor tidak akan bercabang
Dengan menggunakan pohon faktor, yaitu membagi bilangan dengan angka prima secara urut dari 2, 3, 5, 7, hingga dirinya sendiri. Angka prima tidak akan dapat dibagi oleh angka prima lain, selain dirinya sendiri dan 1. Hal ini, menyebabkan angka prima tidak dapat membentuk pohon faktor (karena tidak ada cabangnya).
Contoh: 13 hanya dapat dibagi 1 dan 13.
Dengan menggunakan rumus atau cara di atas, kita dapat menentukan suatu angka merupakan prima atau bukan.
E. Kegunaan Bilangan Prima
- Dalam ilmu matematika bilangan prima erat kaitannya dengan tingkat pembelajaran yang lebih tinggi, seperti mencari FPB, menyederhanakan pecahan, dan lain-lain.
- Bilangan prima digunakan dalam ilmu kriptografi (cryptography) untuk melakukan enkripsi data. Aplikasinya memegang peranan yang penting terkait keamanan data, seperti network security, sistem keamanan rekening bank, dan lain-lain.
F. Contoh Soal Bilangan Prima
Berikut beberapa contoh soal bilangan prima, untuk meningkatkan pemahaman materi ini.
-
Mengapa 6 bukan bilangan prima?
Angka 6 bukan bilangan prima karena mempunyai lebih dari 2 faktor pembagi yaitu 1, 2, 3, 6, 1 karena 6 : 1 = 6 2 karena 6 : 2 = 3 3 karena 6 : 3 = 2 6 karena 6 : 6 = 1
-
Mengapa angka 7 termasuk bilangan prima?
Angka 7 termasuk bilangan prima, karena hanya mempunyai 2 faktor pembagi yaitu 1 dan 7, 1 karena 7 : 1 = 7 7 karena 7 : 7 = 1 Tidak ada angka lain yang dapat habis membagi 7
-
Apakah 15 adalah bilangan prima?
Angka 15 tidak merupakan bilangan prima, karena mempunyai lebih dari 2 faktor yaitu 1, 3, 5, 15 1 karena 15 : 1 = 15 3 karena 15 : 3 = 5 5 karena 15 : 5 = 3 15 karena 15 : 15 = 1
-
Sebutkan bilangan prima genap?
Terdapat satu bilangan prima genap, yaitu angka 2. Bilangan ini sekaligus menjadi bilangan prima terkecil.
-
Sebutkan bilangan prima kurang dari 10?
2, 3, 5, 7
-
Sebutkan bilangan prima antara 10 dan 20?
11, 13, 17, 19 Catatan: jika soal menggunakan kata "antara", maka bilangan 10 dan 30 tidak termasuk.
-
Sebutkan bilangan prima 1 sampai 100?
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97,
-
Apakah 1 bilangan prima?
Angka 1 bukanlah bilangan prima karena hanya memiliki 1 faktor saja.
-
Berapakah bilangan prima terbesar yang telah ditemukan?
Secara teori tidak ada bilangan prima terbesar, konsep ini telah dibuktikan oleh matematikawan Euclid. Namun, nilai bilangan prima terbesar terus dicari secara formal oleh organisasi internasional yang bernama GIMPS (Great Internet Mersenne Prime Search). Bahkan organisasi ini menghadiahkan US$3000 untuk peneliti yang dapat menemukan bilangan prima terbesar selanjutnya yang menyentuh 100 juta digit angka. Berdasarkan catatan: Tahun 2019, bilangan prima terbesar adalah 282,589,933 − 1
-
Sebutkan bilangan prima 100 sampai 200?
101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199
Kontributor Materi: Mohammad Nur (Pemeriksa)
Baca juga tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel Pengertian Bilangan Prima. Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih…















bagus
Terima kasih atas penilaiannya kak Septian Mustakim 🙂
Makasih kak aku lebih paham ^^ Thanks you verry much:)
Terima kasih kembali Nazla atas feedback-nya 🙂
makasih kak,konsep materinya bagus 🙂
akhirnya paham huhuhu T_T makasih banyak ka
Hai, Nanai
Senang dapat membantu proses belajarnya 🙂