Bilangan rasional dan irasional merupakan 2 jenis bilangan yang merupakan bagian dari sistem bilangan real (ℝ). Berikut dijelaskan mengenai pengertian, sifat, dan contohnya masing-masing.
Artikel terkait: Bilangan Real | Pengertian Bilangan Real dan Contohnya
Navigasi Cepat:
A. Pengertian Bilangan Rasional (ℚ)
Bilangan rasional adalah sistem bilangan yang merupakan himpunan dari semua bilangan yang dapat dinyatakan dalam bentuk pecahan a/b dengan a, b adalah bilangan bulat dan b ≠ 0. Secara fundamental bilangan rasional berasal dari bahasa inggris yaitu "rational" karena bilangan ini dapat dinyatakan dalam bentuk perbandingan (rasio). Ahli matematika memberikan simbol ℚ untuk bilangan rasional.
Artikel terkait: Pengertian serta Contoh Bilangan Bulat Positif dan Negatif
Misalnya:
Bilangan 1,2 termasuk bilangan rasional, karena dapat dinyatakan dalam bentuk pecahan berikut
1,2 dapat dinyatakan dalam bentuk pecahan 12/10, 6/5, ataupun bentuk pecahan lain yang memenuhi a/b dengan a, b (bilangan bulat) dan b ≠ 0. Sehingga 1,2 termasuk bilangan rasional.
A1. Contoh Bilangan Rasional
| Bilangan | a/b | Rasional |
|---|---|---|
| 0 | 0/1 | Ya |
| 1,2 | 6/5 | Ya |
| 4 | 4/1 | Ya |
| 0,45 | 45/100 | Ya |
| √3 | (tidak ada) | Tidak |
| 30% | 30/100 | Ya |
A2. Sifat-Sifat Bilangan Rasional
Bilangan rasional dapat didefinisikan untuk setiap 
merupakan bilangan rasional dalam bentuk pecahan, maka berlaku sifat-sifat berikut:
-
Dapat dinyatakan dalam bentuk pecahan a/b dengan a, b adalah bilangan bulat dan b ≠ 0
-
Tertutup, terhadap operasi penjumlahan dan perkalian
Penjumlahan dan perkalian antar bilangan rasional juga menghasilkan bilangan rasional.
menghasilkan bilangan rasional.
menghasilkan bilangan rasional. -
Komutatif, terhadap operasi penjumlahan dan perkalian
Penjumlahan dan perkalian antar bilangan rasional mempunyai sifat komutatif, yang dapat dirumuskan sebagai berikut.
-
Asosiatif, terhadap operasi penjumlahan dan perkalian
Penjumlahan dan perkalian antar bilangan rasional mempunyai sifat asosiatif, yang dapat dirumuskan sebagai berikut.
-
Distributif
Bilangan rasional mempunyai sifat distributif, yang dapat dirumuskan sebagai berikut.
-
Punya elemen identitas penjumlahan dan perkalian
- Bentuk
adalah elemen identitas penjumlahan bilangan rasional, karena setiap x bilangan rasional yang dijumlahkan dengan hasilnya adalah x bilangan rasional itu sendiri.
- Bentuk
adalah elemen identitas perkalian bilangan rasional, karena setiap x bilangan rasional yang dikalikan dengan hasilnya x bilangan rasional itu sendiri.
- Bentuk
-
Setiap elemen punya invers terhadap operasi penjumlahan dan perkalian
Setiap bilangan rasional mempunyai elemen invers terhadap operasi penjumlahan dan perkalian. Sehingga setiap bilangan rasional yang dioperasikan dengan invers menghasilkan elemen identitas.
- Bentuk
adalah invers penjumlahan untuk setiap bilangan rasional 
, sehingga berlaku persamaan berikut.
- Bentuk
adalah invers perkalian untuk setiap bilangan rasional ≠ 0, sehingga berlaku persamaan berikut.
- Bentuk
-
Perkalian dengan Nol (0)
Perkalian bilangan rasional dengan angka nol menghasilkan angka nol, sehingga berlaku persamaan berikut.
-
Mempunyai bentuk desimal berulang
Bilangan rasional mempunyai bentuk desimal berulang.
Contoh: 1 = 1,0000000 ... 1/3 = 0,333333 ... 12/11= 1,090909 ... 13/3 = 4,333333 ...
B. Pengertian Bilangan Irasional
Bilangan irasional adalah sistem bilangan yang tidak dapat dinyatakan dalam bentuk pecahan a/b dengan a, b adalah bilangan bulat dan b ≠ 0, namun dapat dinyatakan dalam bentuk desimal.
B1. Contoh Bilangan Irasional dan Penjelasannya
| Bilangan | a/b | irasional |
|---|---|---|
| √2 = 1,4142 ... | Tidak ada | Ya |
| √3 = 1,7320 ... | Tidak ada | Ya |
| √4 = 2 | 2/1 | Tidak |
| π = 3,14159 ... | Mendekati 22/7 | Ya |
| e = 2,71828 ... | Tidak ada | Ya |
| 0,25 | 1/4 | Tidak |
B2. Sifat-Sifat Bilangan Irasional
Secara umum bilangan irasional mempunyai sifat sebagai berikut:
-
Tidak dapat dinyatakan dalam bentuk pecahan a/b dengan a, b adalah bilangan bulat dan b ≠ 0
-
Memenuhi Sifat Komutatif Penjumlahan dan Perkalian
Misalnya a dan b adalah bilangan irasional, maka berlaku sifat komutatif untuk operasi penjumlahan dan perkalian.
Sifat komutatif penjumlahan: a + b = b + a Sifat Komutatif Perkalian: a × b = b × a
-
Memenuhi Sifat Asosiatif Penjumlahan dan Perkalian
Misalnya a, b, dan c adalah bilangan irasional, maka berlaku sifat asosiatif untuk operasi penjumlahan dan perkalian.
Sifat asosiatif penjumlahan: (a + b) + c = a + (b + c) Sifat asosiatif perkalian: (a × b) × c = a × (b × c)
-
Memenuhi Sifat Distributif terhadap Penjumlahan dan Pengurangan
Misalnya a, b, dan c adalah bilangan irasional, maka berlaku sifat distributif.
Sifat distributif terhadap penjumlahan: a × (b + c) = (a × b) + (a × c) Sifat distributif terhadap pengurangan: a × (b – c) = (a × b) – (a × c)
Artikel terkait: Sifat Komutatif, Asosiatif, dan Distributif pada Operasi Hitung
-
Punya Elemen Identitas
Elemen identitas pada bilangan irasional sama dengan elemen identitas pada bilangan real, yaitu 0 untuk operasi penjumlahan dan 1 untuk operasi perkalian.
Contoh: suatu bilangan irasional √2 memenuhi Identitas penjumlahan √2 + 0 = √2 Identitas perkalian √2 × 1 = √2
-
Setiap Elemen Punya Invers
Invers bilangan irasional suatu bilangan dapat dihitung berdasarkan konsep pecahan, perlu dicatat bentuk pecahan a/b bilangan irasional "tidak memenuhi" a dan b = bulat. Perlu diketahui suatu bilangan yang dioperasikan dengan suatu operasi dengan inversnya menghasilkan elemen identitas operasi yang digunakan.
Contoh:
Π adalah bilangan irasional yang dapat ditulis sebagai Π/1. Maka invers perkalian dari Π adalah 1/Π Maka invers penjumlahan dari Π adalah -Π
√3 adalah bilangan irasional yang dapat ditulis sebagai √3/1. Maka invers perkalian dari √3 adalah 1/√3 Maka invers penjumlahan dari √3 adalah -√3
-
Operasi Perkalian dengan Nol menghasilkan Nol
Setiap bilangan irasional yang dikalikan dengan nol akan menghasilkan angka nol.
-
Tidak mempunyai bentuk desimal berulang
Bilangan irasional tidak membentuk pola berulang
Contoh √2 = 1,414213562373095048801688724209698078569671875376948073176679737990732478462107038850387534327641572735013846230912297024924836055850737212644121497099935831... Hingga digit ke-2 juta, pola berulang dari √2 belum juga ditemukan.
Perhitungan dilakukan oleh Robert Nemiroff (George Mason University and NASA Goddard Space Flight Center) dan diperiksa oleh Jerry Bonnell (University Space Research Association and NASA Goddard Space Flight Center).
-
Mempunyai bentuk akar tidak sempurna dengan hasil desimal tidak berulang
Bentuk akar tidak sempurna adalah bentuk akar yang menghasilkan nilai tidak bulat.
Contoh:
√2 = 1.4142135... √3 = 1.7320508... √5 = 2.236067...
-
Mempunyai sifat tidak tertutup
Sifat tidak tertutup pada bilangan irasional disebabkan karena operasi penjumlahan dan perkalian antar bilangan irasional dapat menghasilkan bilangan rasional.
Contoh:
√2 × √2 = √4 = 2; hasil rasional √2 × √3 = √6; hasil tetap irasional
Baca juga tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel “Pengertian Bilangan Rasional dan Irasional serta Contohnya“. Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih…
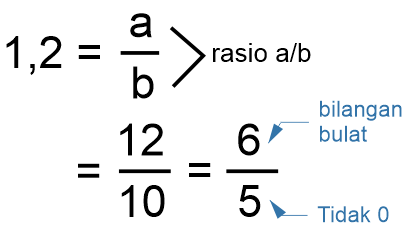
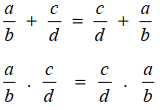
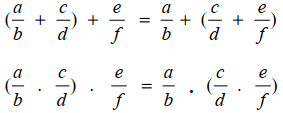
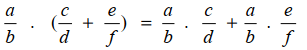
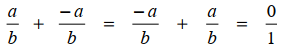
Apakah 1/4 dan 2/3 merupakan bilangan real
1/4 dan 2/3 adalah bilangan real, kedua pecahan tersebut juga termasuk bilangan rasional karena dapat dinyatakan dalam bentuk a/b. Sebagaimana kita ketahui bilangan real memuat seluruh bilangan rasional dan irasional.
Baca lebih lanjut: Materi Bilangan Real
Semoga bermanfaat Wike 🙂
10/3 irrasional?
Hai Annisa
10/3 itu bilangan rasional karena dapat dibentuk ke pecahan a/b dengan a=10 dan b=3,
Secara bentuk desimal dari 10/3=3.333333.... memuat desimal berulang, salah satu ciri bilangan rasional yaitu bentuk desimal berulang.
Semoga bermanfaat 🙂
Kak, 2√3 kenapa bilangan irasional. Tolong penjelasnnya🙏
Hai Dilla Arista,
Angka 2√3 = 2 * √3 = √4 (rasional) * √3 (irasional) = √12 = 3.464101615137755... (Bentuk Akar tidak sempurna dengan hasil tidak berulang adalah bilangan irasional).
Dapat disimpulkan, perkalian bilangan rasional dengan irasional menghasilkan bilangan irasional.
Semoga bermanfaat 🙂
Lalu apakah bilangan pecahan yang hasilnya tidak dalam bentuk desimal berulang disebut bilangan rasional
Hai Dian,
Bilangan pecahan a/b yang memenuhi a,b = bilangan bulat dan b tidak 0, dipastikan selalu menghasilkan bilangan dengan desimal berulang.
Semoga bermanfaat 🙂
Komutatif, Asosiatif, Distributif, Punya Elemen Identitas, Setiap Elemen Punya Invers, dan Operasi Perkalian dengan Nol menghasilkan Nol maksudnya bagaimana dan contohnya seperti apa ?
Hai kak Aisiyah Panjani, Artikelnya sudah ditambahkan materi terkait...
Terima kasih banyak atas reviewnya 🙂
Terimakasih ka, materinya jadi mudah ntuk dipahamin deh 🙂
Sama-sama Aisiyah Panjani 🙏
Senang dapat membantu 🙂
kak. mau nanya ini bener atau tidak. akar 2 = 1,41421. 1,41421 kan hasil dari 141.421 per 100.000. mohonpenjelasannya..
halo kak,apakah 1,345346347348349... merupakan bilangan rasional?
Berikan contoh menghitung nilai hampiran bilangan irasional.
Hai, Meriani Hermina
Contohnya π (phi) menghampiri 3,14 atau 22/7
Semoga membantu 🙂
Kak Mohon dong
Cantukan referensi buat tugas kuliah
Hai, Kak Inessrisuryana
Untuk informasi spesifik terkait pos klik "Tampilkan Informasi Post" di bawah artikel ini
Untuk referensi tertulis dapat membuka halaman bibliography
Semoga membantu 😉
Artikel ini bisa dijadikan referensi
mohon ijin dan terimakasih sangat membantu..
Hai, Kak Tika Ayu
Sebagai pengelola saya sangat senang mendengarnya
Senang dapat membantu belajar Matematika 🙂
halo, mengapa bilangan eksponensial termasuk irasional ya? mohon penjelaannya.... terimakasih