A. Pengertian Fungsi Kuadrat
Fungsi kuadrat adalah fungsi yang disusun oleh persamaan kuadrat berbentuk umum f(x) = ax² + bx + c, dengan a ≠ 0. Grafik fungsi kuadrat berbentuk non-linear dalam koordinat kartesius yaitu berupa parabola. Garis non-linear adalah istilah untuk garis tidak lurus dalam ilmu matematika. Fungsi kuadrat dalam bahasa inggris disebut dengan "Quadratic Function". Konsep fungsi kuadrat menggunakan konsep yang sama dengan konsep persamaan kuadrat yang dipelajari ditingkat sebelumnya.
Sebelumnya: Pengertian Persamaan Kuadrat, Bentuk Umum, Rumus, dan Akar-Akar Persamaan Kuadrat
Navigasi Cepat
- A. Pengertian Fungsi Kuadrat
- B. Sifat-Sifat Grafik Fungsi Kuadrat
- C. Cara Menggambar Grafik Fungsi Kuadrat dan Contohnya
A1. Bentuk Umum Fungsi Kuadrat
Berikut bentuk umum fungsi kuadrat
f(x) = ax² + bx + c atau dalam bentuk koordinat kartesius ⇔ y = ax² + bx + c atau dalam bentuk relasi fungsi f : x → ax² + bx + c
dengan
a = koefisien variabel x², dengan a ≠ 0
Nilai koefisien a dalam bentuk fungsi kuadrat menentukan jenis bentuk grafik non-linear yang dibentuk, yaitu:
a < 0 menghasilkan parabola membuka ke atas
a > 0 menghasilkan parabola membuka ke bawah
b = menyatakan koefisien x dari fungsi kuadrat
c = menyatakan konstanta fungsi kuadrat
Nilai koefisien c dalam bentuk fungsi kuadrat menentukan titik potong grafik terhadap sumbu y dari fungsi kuadrat dalam koordinat kartesius.
A2. Contoh Fungsi Kuadrat
Berikut beberapa contoh fungsi kuadrat.
- f(x) = x²
- y = -2x²
- f(x) = 2x² + x
- y = 7x² + 2x + 3
- f(x) = 3x² + 1
- y = -3x² + 3x + 1
- 2y = x² + 2x + 1
Pada contoh di atas 2y = x² + 2x + 1 merupakan bentuk fungsi kuadrat yang tidak sesuai dengan bentuk umum fungsi kuadrat. Sehingga untuk membuat grafiknya, sebaiknya bentuk tersebut diubah ke dalam bentuk umumnya untuk mempermudah penggambaran. Untuk mengubahnya ke bentuk umum, nilai koefisien y sebaiknya dibuat menjadi satu.
2y = x² + 2x + 1 Untuk mengubah koefisien y dari 2 menjadi 1, kedua ruas dibagi dengan ÷2 Sehingga diperoleh ⇔ 2y = x² + 2x + 1 2 ⇔ y = 1/2x² + x + 1/2
B. Sifat-Sifat Grafik Fungsi Kuadrat
Grafik dari fungsi kuadrat dalam koordinat kartesius berbentuk non-linier yaitu kurva parabola. Sebelum suatu fungsi kuadrat dibuat grafiknya, sebaiknya bentuknya disesuaikan dengan bentuk umumnya, yaitu dengan nilai koefisien y = 1.
Berikut beberapa sifat-sifat grafik fungsi kuadrat berdasarkan bentuk umumnya.
B1. Nilai a: Bentuk Parabola Fungsi Kuadrat
Bentuk parabola fungsi kuadrat ditentukan nilai koefisien a dalam bentuk umum f(x) = ax² + bx + c, yaitu:
a > 0 kurva parabola membuka ke atas (a positif)
a < 0 kurva parabola membuka ke bawah (a negatif)
Berikut ilustrasinya,
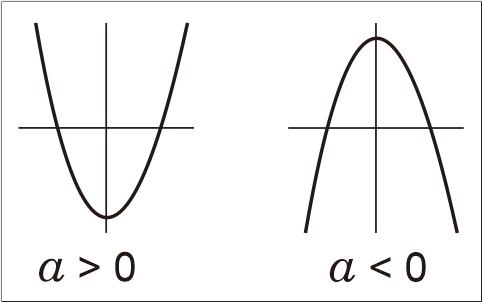
Contoh:
Contoh a > 0: y = x + x - 3, maka kurva membuka ke atas Contoh a < 0: y = -x + x - 3, maka kurva membuka ke bawah
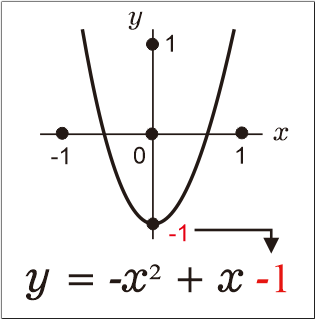
B2. Nilai c: Titik Potong Sumbu y Grafik Fungsi Kuadrat
Titik potong grafik fungsi kuadrat ditentukan oleh nilai konstanta c, pada bentuk umum fungsi kuadrat ax² + bx + c. Nilai konstanta c merupakan titik potong sumbu y dari kurva yang dibentuk fungsi kuadrat, yaitu titik (0, c)
Contoh:
B3. Titik Ekstrim: Titik Puncak Grafik Fungsi Kuadrat
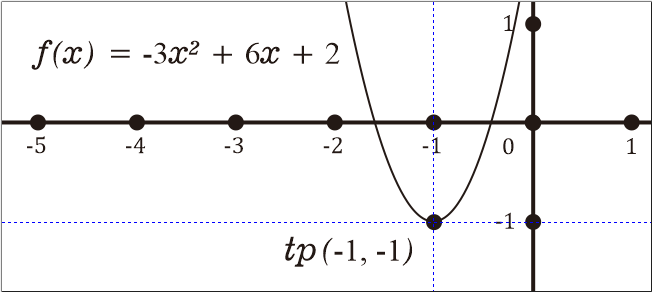
Titik puncak grafik parabola dari fungsi kuadrat dapat dihitung dari bentuk umumnya ax² + bx + c. Titik puncak kurva parabola juga disebut titik ekstrim.
Berikut rumus untuk mencari titik puncak grafik fungsi kuadrat, yaitu hitung titik ekstrim di sumbu x, lalu hitung nilai fungsinya untuk mendapat titik ekstrim sumbu y.
Contoh:
Diketahui sebuah fungsi kuadrat f(x) = 3x² + 6x + 2, tentukan titip puncak dari grafiknya!
Sehingga titik puncak grafik tersebut berada pada titik (-1, -1), berikut ilustrasinya.
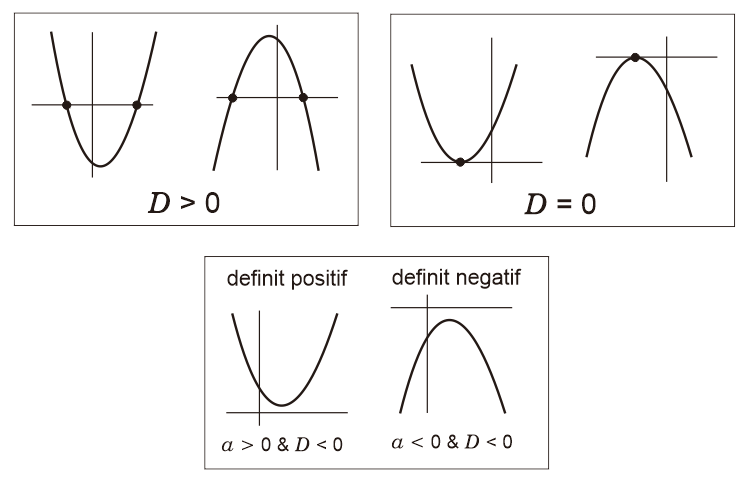
B4. Nilai Determinan: Karakteristik Grafik Fungsi Kuadrat
Nilai determinan fungsi kuadrat ax² + bx + c adalah D = b² - 4ac. Nilai determinan suatu fungsi kuadrat dapat digunakan sebagai parameter karakteristik grafik berdasarkan titik potongnya di sumbu x.
Dengan karakteristik grafik fungsi kuadrat berdasarkan nilai determinannya (D) sebagai berikut.
- D > 0; berarti grafik fungsi kuadrat mempunyai dua akar real berbeda (grafik memotong sumbu x di dua titik yang berbeda).
- D = 0; berarti grafik fungsi kuadrat mempunyai dua akar real kembar (grafik memotong sumbu x pada satu titik dan merupakan sebuah titik puncak).
- D < 0; berarti grafik fungsi kuadrat mempunyai akar imaginer (grafik tidak memotong sumbu x).Terdapat 2 jenis karakteristik grafik kuadrat saat nilai D < 0, yaitu:
- Definit positif saat a > 0 dan D < 0 adalah karakteristik grafik kuadrat saat posisinya berada di atas sumbu x.
- Definit negatif saat a < 0 dan D < 0 adalah sebutan karakteristik grafik kuadrat saat posisinya berada di bawah sumbu x.
Berikut ilustrasi grafik fungsi kuadrat berdasarkan nilai determinannya.
B5. Akar-Akar: Titik Potong Grafik Kuadrat di Sumbu x
Nilai determinan dapat digunakan untuk melihat secara umum perpotongan grafik kuadrat terhadap sumbu x. Titip potong grafik kuadrat terhadap sumbu x dapat diketahui dengan menghitung nilai akar-akarnya. Sebelum menghitung titip potong terhadap sumbu x, perlu dipastikan nilai determinannya, yaitu:
- D > 0, hitung akar-akar fungsi kuadrat untuk menemukan titik potong grafik terhadap sumbu x
- D = 0, titik potong grafik fungsi kuadrat dengan sumbu x sama dengan titik puncaknya
- D < 0, grafik fungsi kuadrat tidak berpotongan dengan sumbu x
Saat D > 0, hitung titik potong sumbu x dengan mencari akar-akar kuadratnya. Berikut beberapa metode persamaan kuadrat untuk menghitung akar-akar fungsi kuadrat.
Contoh:
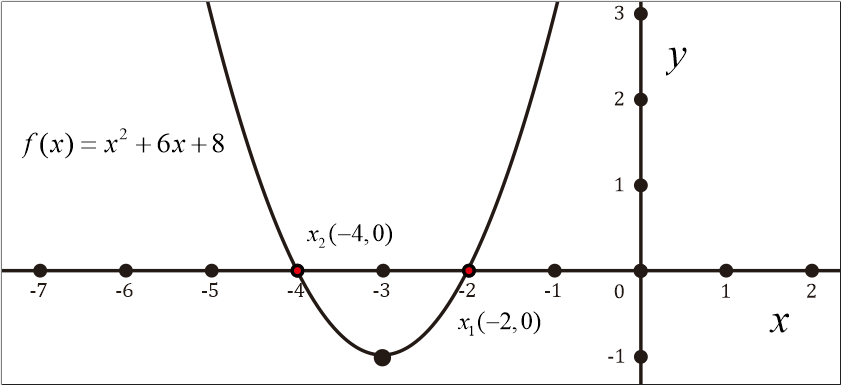
Carilah titik potong dari fungsi kuadrat f(x) = x² + 6x + 8
Penyelesaian:
Fungsi f(x) = x² + 6x + 8, berdasarkan bentuk umum diperoleh'
a = 1; b = 6; dan c = 8
#Menentukan karakteristik grafik kuadrat dengan nilai determinan
D = b² - 4ac = (6)² - 4(1)(8) = 36 - 32 = 4 Diperoleh D = 4 memenuhi D > 0 Sehingga fungsi kuadrat mempunyai 2 akar real yang berbeda, dalam bentuk grafik akan memotong sumbu x di 2 titik yang berbeda.
# Menghitung titik potong terhadap sumbu x
Karena D > 0, maka dilanjutkan dengan menghitung akar-akar persamaan kuadrat
Berikut dihitung akar-akar persamaan kuadrat dengan menggunakan metode faktorisasi
Sehingga dapat dihitung akar-akar persamaan kuadratnya
Diperoleh, akar-akar persamaan kuadrat dari x² + 6x + 8 = 0 adalah
x1 = -2 dan x2 = -4.
Sehingga titik potong sumbu x dari grafik fungsi f(x) = x² + 6x + 8 adalah x1 = -2 dan x2 = -4.
Berikut ilustrasi grafik dalam koordinat kartesius.
C. Cara Menggambar Grafik Fungsi Kuadrat dan Contohnya
Berdasarkan pemaparan di bagian B yaitu sifat-sifat grafik fungsi kuadrat, dapat diketahui langkah-langkah menggambar grafik fungsi kuadrat, yaitu:
-
Cek nilai a
- a > 0 maka parabola membuka ke atas
- a < 0 maka parabola membuka ke bawah
-
Cek konstanta c
- Nilai c merupakan titik potong grafik di sumbu y yaitu (0, c)
-
Hitung titik puncak
-
Hitung determinan (D)
- D = b² - 4ac
- D > 0, memotong sumbu x di dua titik berbeda
- D = 0, memotong sumbu x di satu titik tepatnya di titik puncak
- D < 0, tidak memotong sumbu x
- D = b² - 4ac
-
Jika D > 0, hitung titik potong dengan mencari akar-akar persamaan kuadrat
-
Tandai titik potong sumbu x, y, dan titik puncak
-
Lakukan substitusi diskrit x ke fungsi dengan interval titik-titik potong dan titik puncaknya (bebas) dan tandai titiknya
-
Gambar grafik fungsi
Contoh:
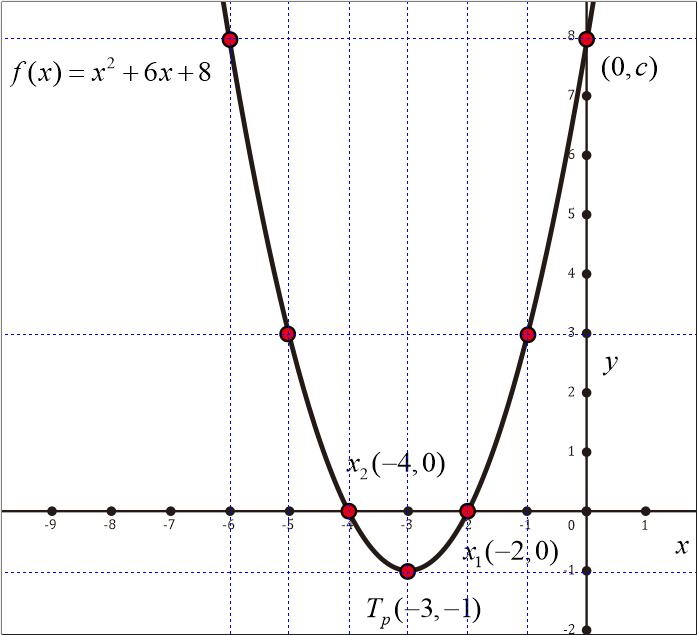
Buatlah grafik dari fungsi kuadrat f(x) = x² + 6x + 8 = 0
Penyelesaian:
Diperoleh nilai a = 1; b = 6; dan c = 8
# Nilai a = 1, maka a > 1, sehingga grafik membuka ke atas
# Nilai c = 8, maka grafik memotong sumbu y di titik (0, 8)
# Perhitungan titik puncak
# Perhitungan Determinan (D)
D = b² - 4ac = (6)² - 4(1)(8) = 36 - 32 = 4 Karena D = 4, maka D > 4 grafik memotong sumbu x di dua titik yang berbeda
# Nilai D > 0, titik potong dihitung mencari akar-akar fungsi kuadrat
Dengan menggunakan metode faktorisasi, diperoleh fungsi f(x) = x² + 6x + 8 mempunyai akar-akar di x1 = -2 dan x2 = -4.
Sehingga titik potong sumbu x dari grafik fungsi f(x) = x² + 6x + 8 adalah x1 = -2 dan x2 = -4.
# Tandai titik potong sumbu x, y, dan titik puncak
# Substitusi diskrit nilai x terhadap fungsi
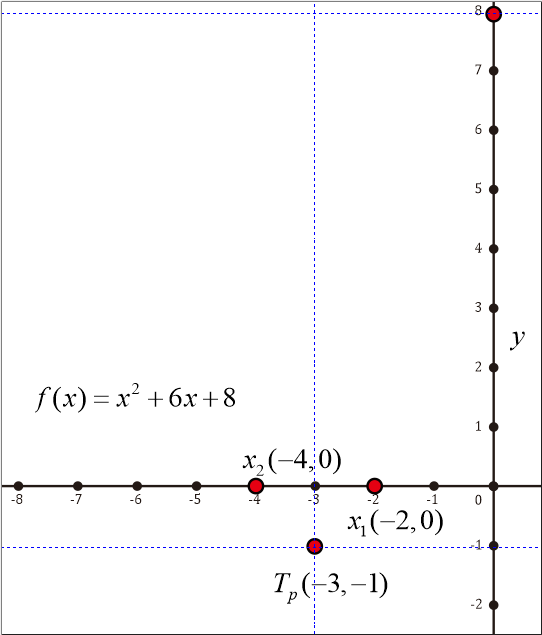
Untuk membuat grafik yang digambar menampilkan informasi titik potong sumbu x, y, dan titik puncak, maka disubstitusikan nilai x yang dapat menggambarkan titik tersebut yaitu [-6, 0] dengan jarak antar titik 1.
x = -6 y = -6² + 6(-6) + 8 = 8 Diperoleh titik (-6, 8) x = -5 y = -5² + 6(-5) + 8 = 3 Diperoleh titik (-5, 3) x = -4 (akar real, jika disubstitusikan nilai pasti 0) Diperoleh titik (-4, 0) x = -3 (titik potong) Diperoleh Tp (-3, -1) x = -2 (akar real, jika disubstitusikan nilai pasti 0) Diperoleh titik (-2, 0) x = -1 y = -1² + 6(-1) + 8 = -3 x = 0 (titik potong di sumbu y, nilai substitusi = c) Diperoleh titik (0, 8)
Sehingga diperoleh
| x | -6 | -5 | -4 | -3 | -2 | -1 | 0 |
| f(x) | 8 | 3 | 0 | -1 | 0 | 3 | 8 |
# Menggambar grafik fungsi kuadrat dengan menarik garis lengkung dari titik-titik potong, titik puncak, dan titik-titik hasil substitusi
Sehingga diperoleh gambar grafik berikut
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel "Fungsi Kuadrat, Rumus, dan Grafik Fungsi Kuadrat". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih...


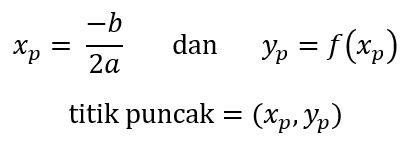

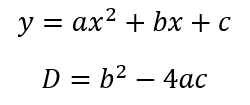

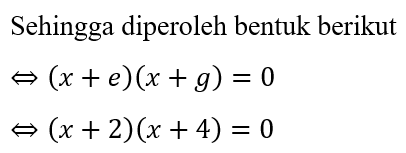
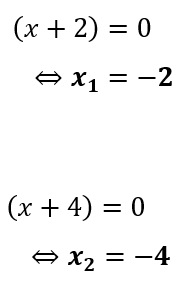
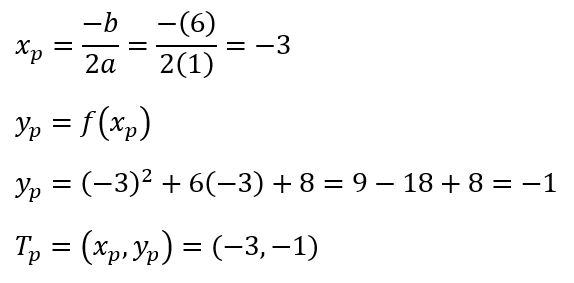







Mohon pencerahannya tentang penggunaan istilah.
Determinan dan Deskriminan
Derminan bisa pada matriks ordo 2x2 |A|=perkalian eentry diagonal utama - perkalian entry diagonal lainnya.
Deskriminan bisa digunakan pada fungsi kuadrat ini, D=b^2-4ac, apa ada kekeliruan saya dalam penggunaan istilah ini?