Pengertian Garis Sejajar, Garis Berpotongan, Tegak Lurus, dan Berimpit

Sifat-sifat garis di bidang geometri ditentukan oleh kedudukannya terhadap garis lainnya, yang terdiri dari garis sejajar, garis berpotongan, garis tegak lurus, dan garis berimpit. Berikut akan dijelaskan ke-4 sifat kedudukan antar garis tersebut.

Artikel terkait: Pengertian Garis Titik Bidang dan Ruang beserta Contohnya

A. Garis Sejajar

Garis sejajar adalah suatu kedudukan dua garis pada bidang datar yang tidak mempunyai titik potong walaupun kedua garis diperpanjang. Secara geometri kesejajaran garis tidak akan pernah bertemu satu dengan lainnya karena mempunyai kemiringan (gradien) yang sama. Garis-garis sejajar tidak harus sama panjang.

Contoh garis sejajar:

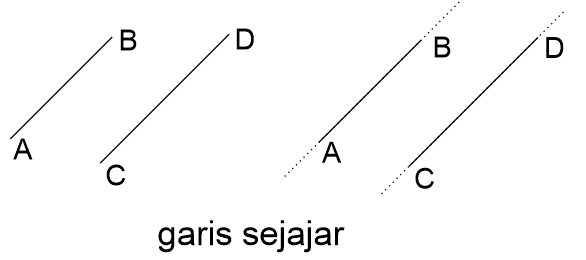
Contoh garis tidak sejajar:

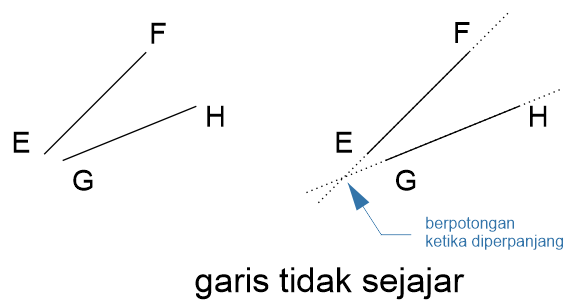
B. Garis Berpotongan

Garis berpotongan adalah kedudukan dua garis yang mempunyai titik potong karena kedua garis saling bertemu. Secara geometri garis-garis yang berpotongan terjadi karena mempunyai kemiringan yang berbeda dan panjang antar garis memungkinkan untuk saling bertemu. Garis yang berpotongan sudah pasti tidak sejajar, namun garis tidak sejajar belum tentu berpotongan.

Contoh garis berpotongan:

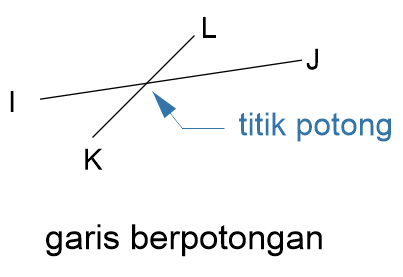
C. Garis Tegak Lurus

Garis tegak lurus adalah kedudukan garis yang berpotongan dan pada titik potongnya terbentuk sudut siku-siku (90°). Garis tegak lurus juga disebut dengan garis serenjang atau garis perpendikular. Dalam simbol matematika garis tegak lurus disimbolkan dengan simbol perpendikular "⊥", misalnya garis MN tegak lurus dengan OP dapat ditulis MN ⊥ OP.

Contoh garis tegak lurus:

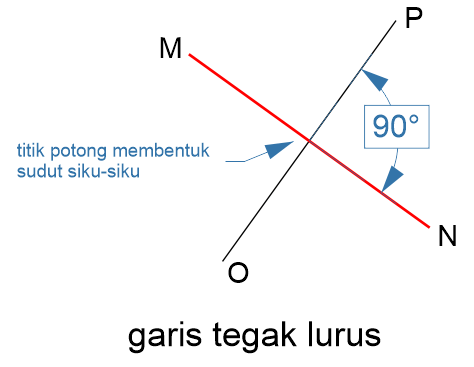
Perkalian dua kemiringan (gradien) garis tegak lurus adalah -1 atau memenuhi persamaan M₁ × M₂ = -1.

Jika, M1 = a/b maka M2 = - b/a

* Karena berlaku
M1 × M2 = a/b × (- b/a) = - ab/ab = -1

Contoh: 
Kemiringan garis MN adalah M1 = 2/3, berapakah kemiringan garis OP di atas?

Penyelesaian:
Karena garis OP ⊥ NM maka gradien garis OP = M2 dihitung memenuhi persamaan M1 × M2 = a/b × (- b/a) = -1 

M1 = a/b = 2/3
a = 2
b = 3
M2 = - b/a = - 3/2 

Jadi, gradien garis OP adalah - 3/2

D. Garis Berimpit

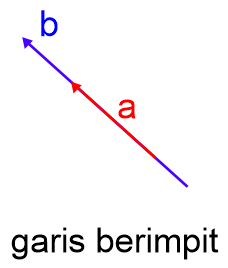
Garis berimpit adalah kedudukan garis yang saling menutupi antara satu dengan lainnya, sehingga garis berimpit tidak dapat dilihat dengan kasat mata. Garis berimpit dapat terjadi karena posisi garis yang sama, namun 2 garis berimpit belum tentu mempunyai panjang yang sama.

Contoh garis berimpit:

Baca juga tutorial lainnya: Daftar Isi Pelajaran Matematika

Sekian artikel "Pengertian Garis Sejajar, Garis Berpotongan, Tegak Lurus, dan Berimpit". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih…