A. Faktorisasi dan Akar Persamaan Kuadrat
Faktorisasi persamaan kuadrat adalah dekomposisi persamaan kuadrat dengan menggunakan faktor-faktor penyusunnya. Dekomposisi persamaan merupakan pengubahan susunan dan struktur suatu bentuk persamaan menjadi bentuk baru yang sebanding.
Akar-akar persamaan kuadrat adalah solusi penyelesaian dari suatu bentuk persamaan kuadrat. Sehingga ketika disubstitusikan hasil persamaannya menghasilkan nilai nol. Solusi ini dapat dihitung menggunakan bentuk faktorisasi persamaannya.
Navigasi Cepat
B. Metode Faktorisasi dan Mencari Akar Persamaan Kuadrat
Berikut 4 cara yang dapat digunakan untuk melakukan faktorisasi persamaan kuadrat, yaitu metode faktorisasi bentuk umum (trinomial), kuadrat murni (pure quadratic), selisih kuadrat (difference of squares), dan solusi nol (zero solution).
| Faktorisasi | Contoh Persamaan Kuadrat |
|---|---|
| Bentuk Umum (Trinomial) | 6x² + 11x – 10 = (3x – 2)(2x + 5) |
| Kuadrat Murni (Pure Quadratic) | 6x² + 9x = 3x(2x + 3) |
| Selisih Kuadrat (Difference of Squares) | 9x² – 16y² = (3x – 4y)(3x + 4y) |
| Solusi Nol (Zero Solution) | ax² = 0; maka x1,2 = 0 |
Baca juga: Materi Dasar Persamaan Kuadrat dan Akar-Akar Penyelesaiannya
# Alternatif Solusi Irasional atau Kompleks
Penggunaan metode faktorisasi dapat menjadi sulit untuk mencari akar-akar persamaan kuadrat, karena solusinya merupakan bilangan irasional dan kompleks. Kasus ini dapat dipermudah dengan menggunakan metode melengkapi kuadrat sempurna atau rumus ABC.
B1. Faktorisasi Bentuk Umum (Trinomial)
Faktorisasi bentuk umum (trinomial) adalah metode untuk mencari akar-akar dan bentuk faktor dari persamaan kuadrat trinomial. Cara ini juga dapat diterapkan untuk persamaan kuadrat trinomial tidak lengkap, misalnya tanpa nilai c atau b dengan menggunakan nilai nol untuk variabel tersebut.
Berikut bentuk umum persamaan kuadrat.
dengan
a = koefisien variabel x² b = koefisien variabel x c = nilai suatu konstanta dengan a ≠ 0
Faktorisasi trinomial dilakukan dengan melakukan perhitungan berikut.
Terdapat beberapa bentuk kuadrat yang tidak mempunyai nilai b atau c, gunakan nilai nol dalam rumus, berikut contohnya.
| Persamaan | a | b | c |
|---|---|---|---|
| 2x² + 3x - 4 = 0 | 2 | 3 | -4 |
| 4x² + 3x = 0 | 4 | 3 | 0 |
| 25x² + 9 = 0 | 25 | 0 | 9 |
Contoh 1. Berapa akar-akar persamaan kuadrat x² + 6x + 8 = 0?
Penyelesaian:
Berdasarkan bentuk umum didefinisikan
a = 1; b = 6; dan c = 8
Sehingga dapat dihitung akar-akar persamaan kuadratnya
∴ Jadi, akar-akar persamaan kuadrat dari x² + 6x + 8 = 0 adalah
x1 = -2 dan x2 = -4.
Contoh 2. Berapa akar-akar persamaan kuadrat 6x² + 11x - 10 = 0?
Penyelesaian:
Berdasarkan bentuk umum didefinisikan
a = 6; b = 11; dan c = -10
Sehingga dapat dihitung akar-akar persamaan kuadratnya
∴ Jadi, akar-akar persamaan kuadrat dari 6x² + 11x - 10 = 0 adalah
x1 = -2/3 dan x2 = -5/2.
B2. Faktorisasi Persamaan Kuadrat Murni
Faktorisasi persamaan kuadrat murni (Pure Quadratic) adalah metode alternatif yang dapat diterapkan untuk faktorisasi persamaan kuadrat murni. Persamaan ini ditandai dengan tidak adanya nilai konstanta c atau konstanta c = 0. Salah satu titik potong persamaan kuadrat murni akan memotong pusat koordinat kartesius di titik (0, 0). Sehingga, dapat dipastikan salah satu nilai akar persamaannya adalah nol.
Metode ini menggunakan nilai koefisien persamaan untuk membentuk persamaan yang sebanding berdasarkan hukum distributif.
Di lain pihak, metode faktorisasi trinomial juga dapat dilakukan untuk menghitung akar-akar persamaan kuadrat murni dengan menggunakan nilai c = 0 dalam perhitungannya.
Contoh 1. Berapa akar-akar persamaan kuadrat 6x² + 9x = 0?
Penyelesaian:
∴ Jadi, akar-akar persamaan kuadrat dari 6x² + 9x = 0 adalah
x1 = -9/6 dan x2 = -11/2.
B3. Faktorisasi Selisih Kuadrat
Faktorisasi selisih kuadrat adalah metode faktorisasi khusus untuk bentuk persamaan dengan selisih kuadrat yaitu ax² - by² = 0. Berikut rumus faktorisasi selisih dua kuadrat (difference of squares).
Metode ini juga dapat diterapkan untuk persamaan kuadrat dengan variabel x² atau y², yang diperlihatkan pada Contoh 2 di subbab ini.
Contoh 1. Berapa akar-akar persamaan kuadrat 6x² + 16y² = 0?
Penyelesaian:
Dari bentuk persamaan kuadrat di atas dapat menggunakan faktorisasi dua kuadrat, sebagai berikut.
Karena persamaan kuadrat tersebut mempunyai dua variabel, solusi akar-akar persamaan dapat ditentukan oleh masing-masing variabel x dan y.
∴ Jadi, diperoleh solusi akar-akar berikut.
Contoh 2. Hitung solusi akar-akar dari persamaan kuadrat 4x² - 36 = 0?
Penyelesaian:
Dari bentuk persamaan kuadrat di atas dapat menggunakan faktorisasi dua kuadrat, sebagai berikut.
Kemudian dihitung solusi akar-akar persamaannya.
∴ Jadi, akar-akar persamaan kuadrat dari 4x² - 36 = 0 adalah
x1 = -3 dan x2 = 3.
B4. Solusi Nol Persamaan Kuadrat ax² = 0
Bentuk persamaan kuadrat ax² = 0 mempunyai solusi akar bernilai nol (zero solution). Nilai solusi x1 = 0 dan x2 = 0 merupakan solusi umum persamaan kuadrat dengan bentuk ax² = 0, berikut pemaparannya.
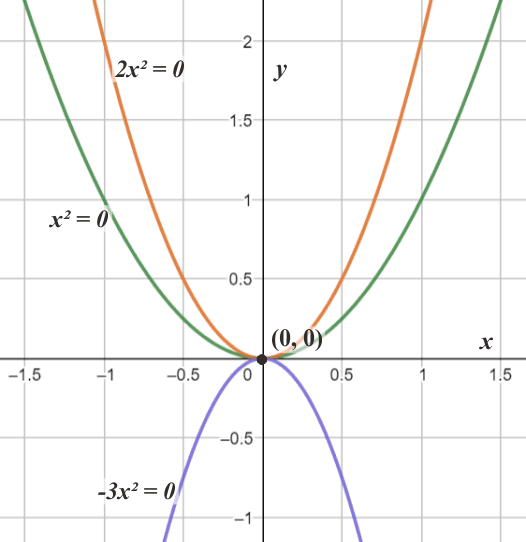
Hal ini juga dapat dibuktikan oleh grafik fungsinya dalam koordinat kartesius, maka akan memotong sumbu koordinat di titik (0, 0). Titik ini juga menjadi titik puncak grafik yang dibentuk.
Contoh 1. Berapa solusi akar-akar persamaan kuadrat dari x² = 0; 2x² = 0; dan -3x² = 0 dan Buatkan grafik fungsinya?
Penyelesaian:
Dapat diketahui titik x = 0 menghasilkan nilai y = 0 di ketiga fungsi kuadrat yang digambarkan dalam grafik, dilihat dari ketiga grafik yang memotong titik pusat (0, 0).
∴ Jadi, akar-akar ketiga persamaan kuadrat tersebut adalah x1,2 = 0.
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel "Faktorisasi Persamaan Kuadrat dan Akar Persamaan Kuadrat". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih...




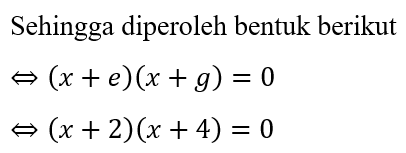
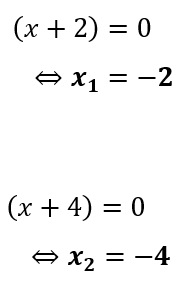


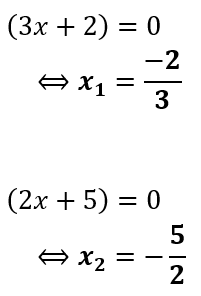


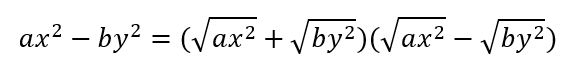




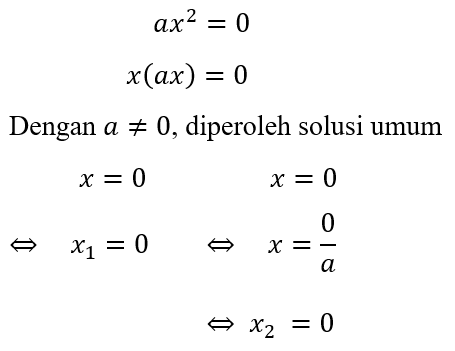







pada mencari akar kuadrat 6x^2 +11x- 10 mengapa saat -4:2 menjadi +2?