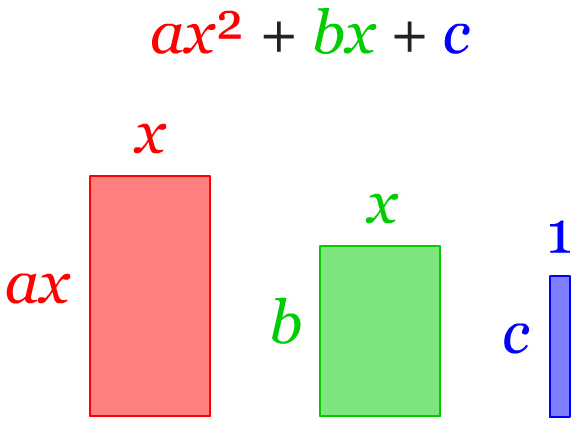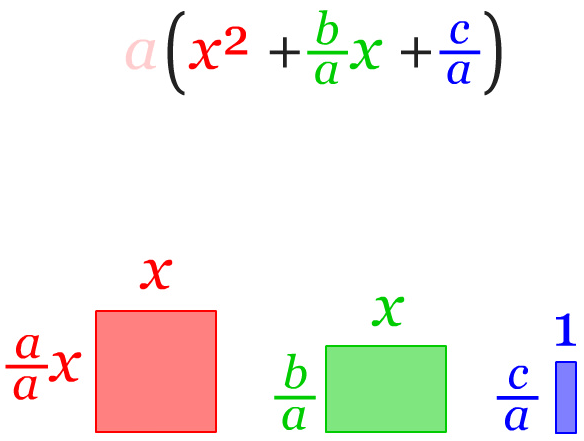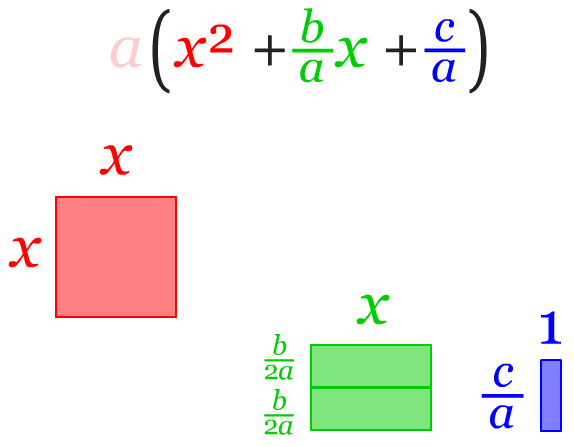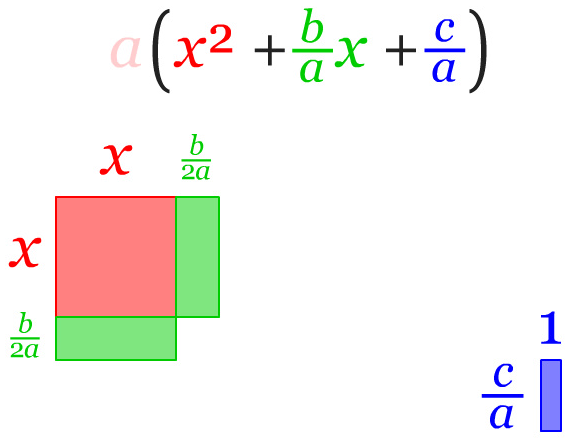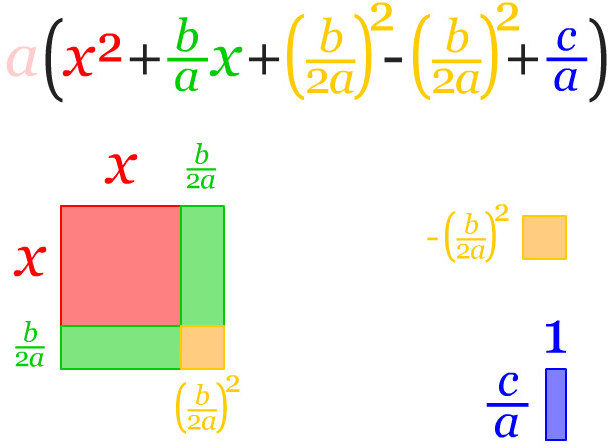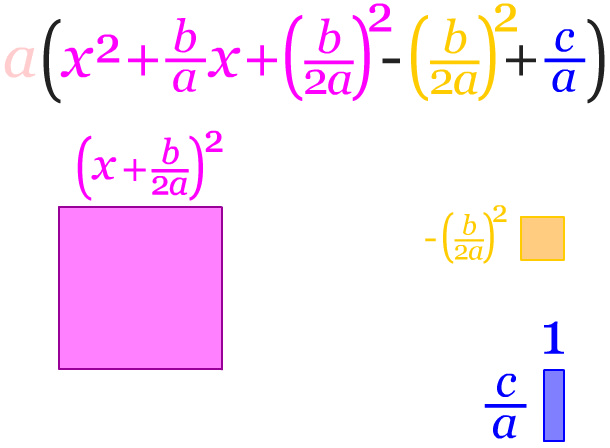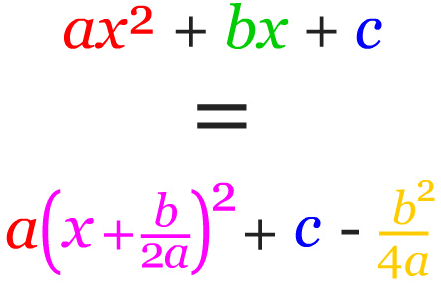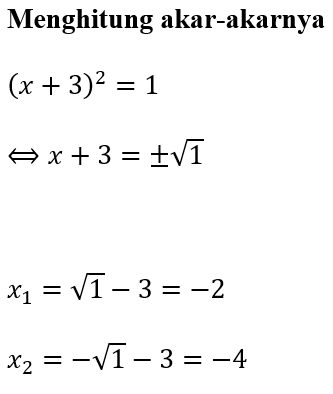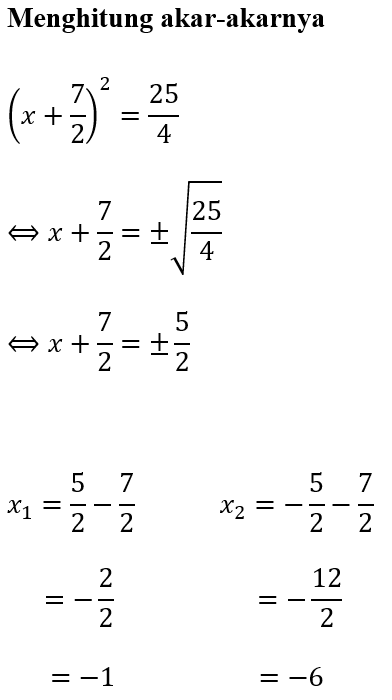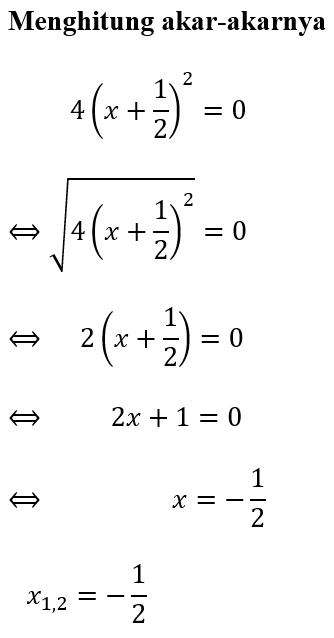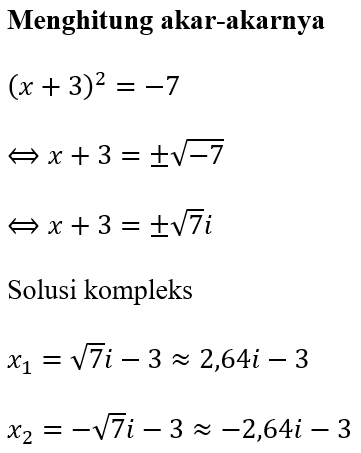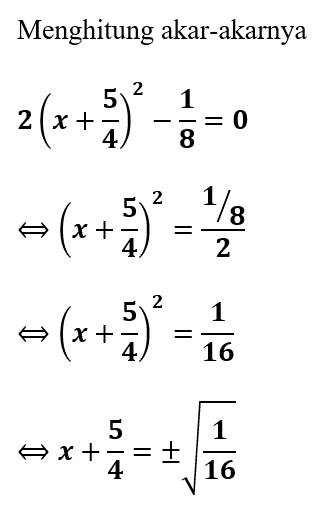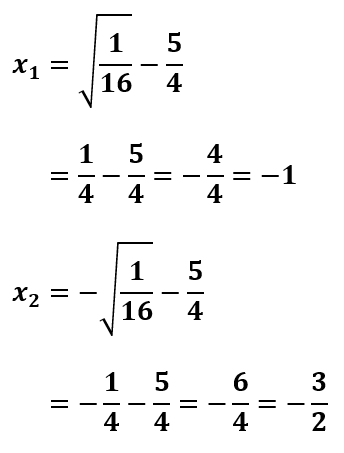A. Rumus Melengkapi Kuadrat Sempurna dan Solusi Akar-Akar
Melengkapi kuadrat sempurna adalah metode yang digunakan untuk mengubah (konversi) bentuk persamaan kuadrat ax² + bx + c = 0 ke bentuk kuadrat sempurna a(x + d)² + e = 0. Metode melengkapi kuadrat sempurna juga disebut dengan metode "completing the square". Berikut rumus metode melengkapi kuadrat sempurna.
Navigasi Cepat
- A. Rumus Melengkapi Kuadrat Sempurna dan Solusi Akar
- B. Pendekatan Geometri: Kuadrat Sempurna
- C. Contoh Soal Melengkapi Kuadrat Sempurna dan Solusinya
B. Pendekatan Geometri: Kuadrat Sempurna
Kuadrat sempurna adalah bentuk persamaan kuadrat yang hanya terdiri dari bentuk kuadrat dan sebuah konstanta. Metode menyempurnakan kuadrat sempurna mengubah bentuk umum persamaan kuadrat ax² + bx + c = 0 menjadi bentuk kuadrat a(x + d)² dan diseimbangkan dengan konstanta e, menjadi a(x + d)² + e = 0. Nilai konstanta e merupakan nilai keseimbangan (equilibrium) terhadap bentuk persamaan kuadrat yang diubah ke dalam bentuk sempurna.
Baca juga: Materi Persamaan Kuadrat, Bentuk, dan Rumus
Metode menyempurnakan kuadrat sempurna digambarkan secara geometri untuk menyeimbangkan bentuk kuadrat dengan persamaan kuadrat yang dikonversi. Bentuk umum persamaan kuadrat dapat digambarkan secara geometri sebagai persegi dan persegi panjang. Bentuk persegi melambangkan bentuk kuadrat dari suatu nilai, koefisien, atau variabel.
Berikut ilustrasi geometri oleh Lucas Vieira (2013) untuk bentuk umum persamaan kuadrat ke bentuk kuadrat sempurna.
Nilai setiap suku dibagi dengan koefisien a, sehingga terbentuk bangun persegi dari suku ax² yaitu ax²/a = x².
Koefisien variabel x dapat dibagi menjadi dua, hasil yang diperoleh berupa dua buah persegi panjang dengan ukuran sisi x dan b/2a. Sehingga dapat dilakukan penggabungan di langkah selanjutnya.
Tiap potongan yang telah dibagi, digabungkan dengan persegi x², sehingga ukurannya pas di sisi kiri dan bawah.
Diperlukan dua selisih nilai yang berlawan untuk membentuk sebuah bangun kuadrat dari gabungan di atas. Pertama, nilai yang memenuhi bentuk bangun gabungan sehingga menjadi bentuk kuadrat yaitu (b/2a)². Kedua, untuk menyeimbangkan persamaan harus dikurangkan dengan nilai tersebut yaitu -(b/2a)².
Sehingga bentuk persegi tersebut dapat formulasikan dalam bentuk kuadrat berikut.
Dapat disederhanakan menjadi bentuk berikut
Langkah sebelumnya yaitu membagi persamaan dengan a. Sekarang kembalikan nilai a tersebut sehingga mencerminkan bentuk persamaan yang sebenarnya dengan mengalikan setiap suku dengan a.
Sehingga diperoleh
C. Contoh Soal Solusi Akar dengan Melengkapi Kuadrat Sempurna
Berikut beberapa contoh soal mencari solusi akar-akar persamaan kuadrat dengan cara melengkapi kuadrat sempurna.
Contoh 1. Hitung Solusi Akar Persamaan x²+6x+8=0 dengan Melengkapi Kuadrat Sempurna!
Penyelesaian:
Sehingga dapat dihitung solusi akar-akarnya, sebagai berikut.
∴ Jadi, akar-akar persamaan kuadrat dari x² + 6x + 8 = 0 adalah
x1 = -2 dan x2 = -4.
Contoh 2. Hitung Solusi Akar Persamaan x²+7x+6=0 dengan Melengkapi Kuadrat Sempurna!
Penyelesaian:
Sehingga dapat dihitung solusi akar-akarnya, sebagai berikut.
∴ Jadi, akar-akar persamaan kuadrat dari x² + 7x + 6 = 0 adalah
x1 = -1 dan x2 = -6.
Contoh 3. Hitung Solusi Akar Persamaan 4x²+4x+1=0 dengan Melengkapi Kuadrat Sempurna!
Penyelesaian:
Sehingga dapat dihitung solusi akar-akarnya, sebagai berikut.
∴ Jadi, akar-akar persamaan kuadrat dari 4x² + 4x + 1 = 0 adalah
x1,2 = -1/2. Solusi ini juga disebut solusi tunggal karena titik potong x1 dan x2 mempunyai nilai sama.
Contoh 4. Hitung Solusi Akar Persamaan x²+6x+16=0 dengan Melengkapi Kuadrat Sempurna!
Penyelesaian:
Sehingga dapat dihitung solusi akar-akarnya, sebagai berikut.
Solusi persamaan tersebut merupakan solusi kompleks, karena perhitungannya terdapat akar kuadrat negatif yang menghasilkan nilai imajiner.
∴ Jadi, akar-akar persamaan kuadrat dari x² + 6x + 16 = 0 adalah
x1 = 2,64i - 3 dan x2 = -2,64i - 3.
Contoh 5. Hitung Solusi Akar Persamaan 2x²+5x+3=0 dengan Melengkapi Kuadrat Sempurna!
Penyelesaian:
Kemudian dapat dihitung akar-akar persamaannya dari bentuk kuadrat sempurna di atas
∴ Jadi, akar-akar persamaan dari 2x² + 5x + 3 = 0 adalah x1 = -1 dan x2 = -3/2.
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel "Melengkapi Kuadrat Sempurna, Solusi Akar, dan Contoh Soal". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih...