A. Pengertian Relasi (Relation)
Relasi adalah himpunan pasangan berurutan dari elemen himpunan daerah asal (domain) ke daerah kawan (kodomain), yang menyatakan adanya hubungan antar elemen-elemennya. Relasi antar himpunan domain ke kodomain dapat digambarkan dalam bentuk diagram panah dan diagram kartesius. Relasi dalam bahasa inggris disebut dengan "relation". Konsep relasi menjadi dasar dari materi fungsi yang dipelajari selanjutnya.
Navigasi Cepat
- A. Pengertian Relasi
- B. Domain, Kodomain, Range, dan Notasi Relasi
- C. Relasi dalam Diagram Panah dan Contohnya
- D. Relasi dalam Diagram Kartesius dan Contohnya
B. Konsep Domain, Kodomain, Range, dan Notasi Relasi
Dalam ilmu matematika, himpunan adalah objek-objek yang didefinisikan dalam suatu kelompok dapat berupa bilangan atau teks. Relasi antar himpunan dapat direpresentasikan dalam bentuk diagram relasi. Beberapa istilah yang penting untuk diketahui untuk membaca diagram relasi adalah domain, kodomain, range, dan notasi relasi.
- Himpunan daerah asal (domain) adalah himpunan pertama yang berhubungan dengan himpunan kedua. Domain dinotasikan sebagai Df.
- Himpunan daerah kawan (kodomain) adalah himpunan kedua yang dihubungkan oleh tanda panah dalam suatu relasi.
- Daerah hasil (range) adalah elemen dari kodomain yang berelasi dengan elemen domain. Range dinotasikan sebagai Rf.
- Notasi relasi didefinisikan dalam tanda silang (cross-sign) yaitu (×), misalnya relasi dari A ke B dapat dinotasikan sebagai A × B.
C. Relasi dalam Diagram Panah dan Contohnya
Relasi antar himpunan dapat digambar dalam bentuk diagram panah. Dalam diagram panah, relasi elemen-elemen himpunan ditunjukkan oleh tanda panah. Himpunan domain digambarkan sebagai himpunan pertama dan himpunan kodomain digambarkan oleh himpunan kedua. Berikut 2 contoh soal diagram panah untuk mempermudah pemahaman.
Contoh C1: Diagram Panah Relasi dengan Elemen Teks
Berikut contoh relasi antara himpunan nama orang (A) yang menjadi domain dengan himpunan nama buah (B) yang menjadi kodomain dalam diagram panah. Elemen-elemen himpunan dalam relasi berikut berupa objek teks.
Tentukan (i) domain, (ii) kodomain, (iii) Range, dan (iv) notasi relasi dari relasi berikut!
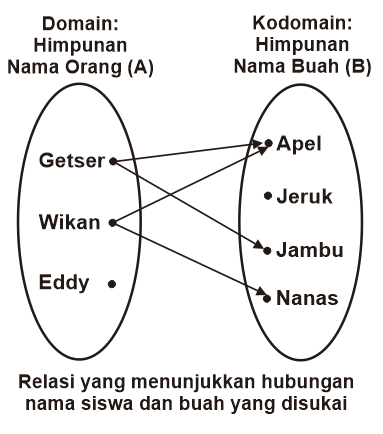
Penyelesaian:
Dari diagram panah di atas dapat diketahui.
(i) Domain (Df)
A = {Getser, Wikan, Eddy}
(ii) Kodomain
B = {Apel, Jeruk, Jambu, Nanas
(iii) Range relasi himpunan A ke B
Range merupakan daerah hasil yaitu elemen kodomain (B) yang berelasi dengan domain (A), yaitu:
Rf = {Apel, Jambu, Nanas}
(iv) Notasi relasi himpunan A ke B
Relasi himpunan dari A ke B ditunjukkan oleh tanda panah di diagram panah dari elemen domain (A) ke kodomain (B), yaitu:
# Getser (Getser, Apel) (Getser, Jambu) # Wikan (Wikan, Apel) (Wikan, Nanas) # Eddy Tidak berelasi
∴ Sehingga, notasi relasi himpunan A ke himpunan B adalah sebagai berikut
A × B = {(Getser, Apel), (Getser, Jambu), (Wikan, Apel), (Wikan, Nanas)}
Contoh C2: Diagram Panah Relasi dengan Elemen Bilangan
Tentukan (i) domain, (ii) kodomain, dan (iii) notasi relasi dari relasi dalam diagram panah berikut.
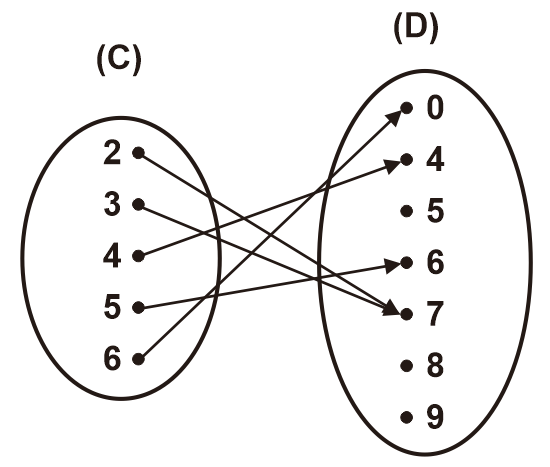
Penyelesaian:
(i) Domain (Df)
C = {2, 3, 4, 5, 6}
(ii) Kodomain
D = {0, 4, 6, 5, 6, 7, 8, 9}
(iii) Range relasi himpunan C ke D
Range merupakan daerah hasil yaitu elemen kodomain (D) yang berelasi dengan domain (A), yaitu:
Rf = {0, 4, 6, 7}
(iv) Notasi relasi himpunan C ke D
Relasi himpunan dari C ke D ditunjukkan oleh tanda panah di diagram panah dari elemen domain (C) ke kodomain (D), yaitu:
# Elemen 2 (2, 7) # Elemen 3 (3, 7) # Elemen 4 (4, 4) # Elemen 5 (5, 6) # Elemen 6 (6, 0)
∴ Sehingga, notasi relasi himpunan C ke himpunan D adalah sebagai berikut
C × D = {(2,7), (3,7), (4,4), (5,6), (6,0)}
D. Relasi dalam Diagram Kartesius dan Contohnya
Relasi antar himpunan juga dapat digambarkan melalui diagram kartesius. Sumbu x (horizontal) pada diagram kartesius menunjukkan domain dan sumbu y (vertikal) menunjukkan kodomain. Kemudian titik-titik potong menunjukkan pasangan elemen yang berelasi.
Baca juga: Pengertian Garis Vertikal dan Horizontal
Penggunaan diagram kartesius disarankan untuk menggambarkan relasi dengan elemen himpunan teks. Saat menggunakan nilai bilangan, titik-titik dalam sumbu kartesius dapat berjarak berjauhan untuk menggambarkan elemen-elemen himpunan yang berelasi. Berikut contoh relasi dalam diagram kartesius untuk mempermudah pemahaman.
Contoh: Diagram Kartesius Relasi dengan Elemen Teks
Diketahui relasi himpunan A ke B yang menyatakan nama siswa dengan pilihan kompetisi mata pelajaran yang diikuti dalam diagram kartesius berikut.
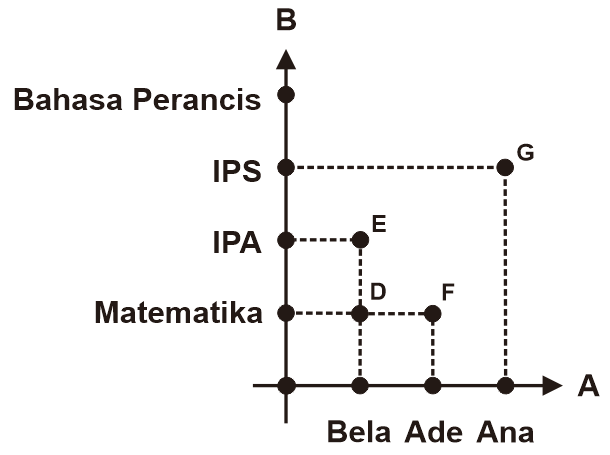
Tentukan (i) domain, (ii) kodomain, (iii) range, dan (iv) notasi relasi dari diagram kartesius tersebut!
Penyelesaian:
(i) Domain (Df)
Himpunan domain berada di sumbu horizontal yaitu himpunan A
A = {Bela, Ade, Ana}
(ii) Kodomain
Himpunan Kodomain berada di sumbu vertikal yaitu himpunan B
B = {Matematika, IPA, IPS, Bahasa Perancis}
(iii) Range
Range dari diagram tersebut merupakan elemen himpunan kodomain yang berhubungan dengan domain, yaitu:
Rf = {Matematika, IPA, IPS}
(iv) Notasi relasi himpunan A ke B
Relasi himpunan A ke B ditunjukkan oleh titik potong dalam diagram kartesius, yaitu:
Titik D: (Bela, Matematika) Titik E: (Bela, IPA) Titik F: (Ade, Matematika) Titik G: (Ana, IPS)
∴ Sehingga notasi relasi himpunan A ke B dalam diagram kartesius tersebut.
A × B = {(Bela,Matematika), (Bela,IPA), (Ade,Matematika), (Ana,IPS)
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel "Apa itu Relasi, Notasi Relasi, Diagram, dan Contohnya". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih...