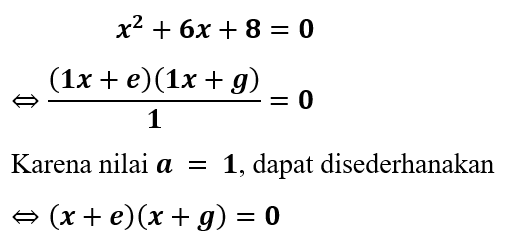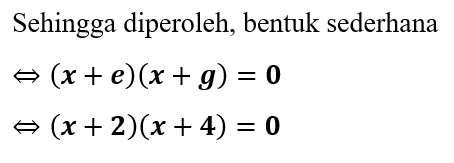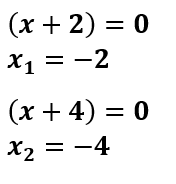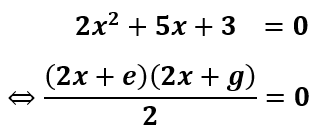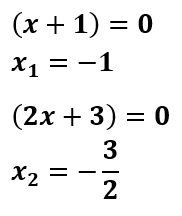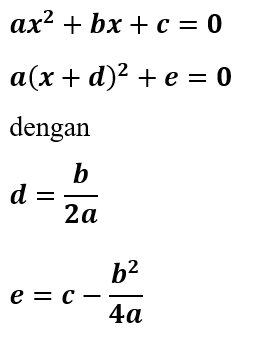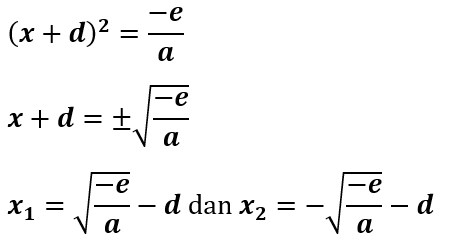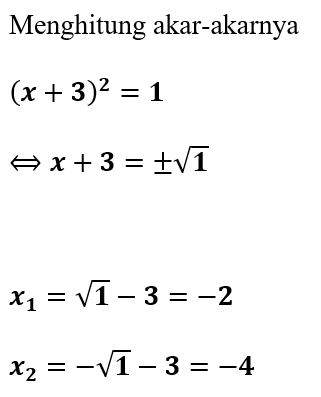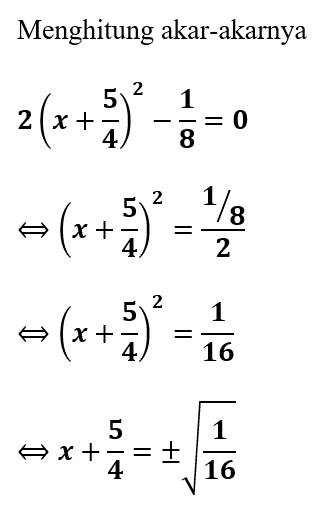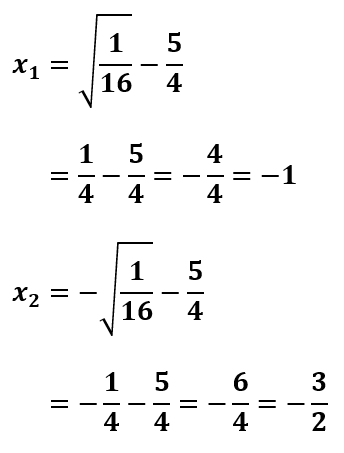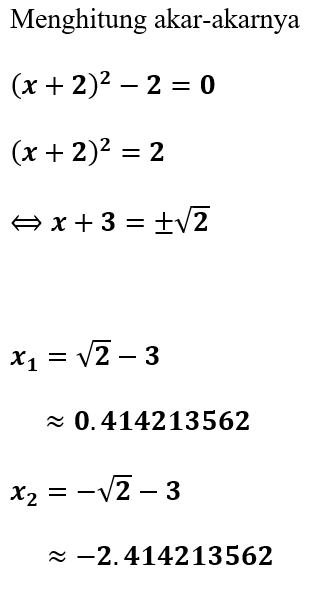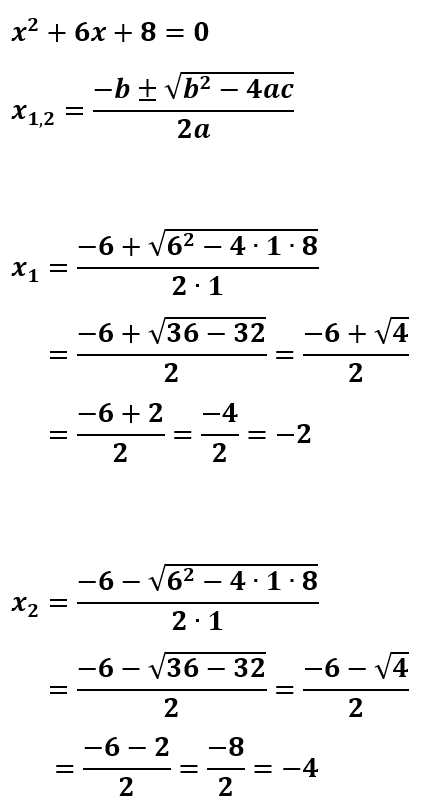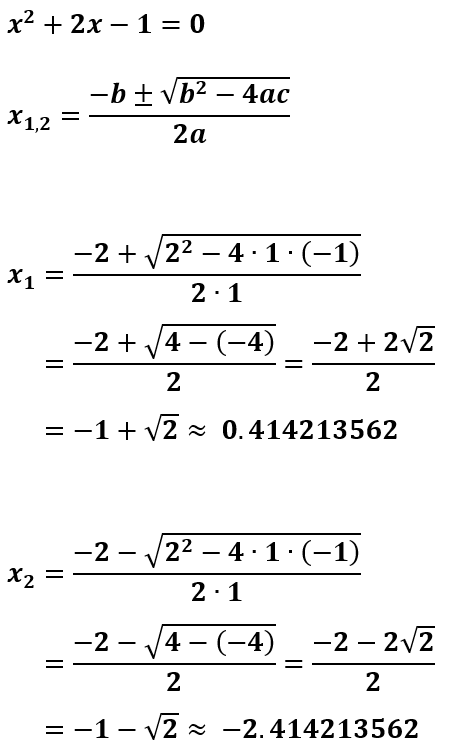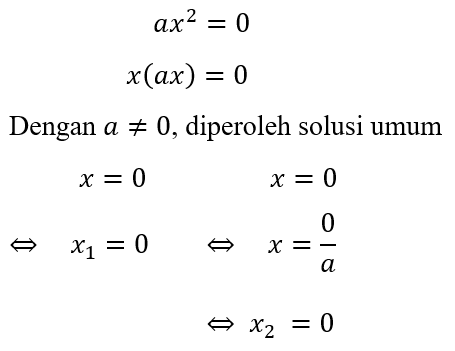A. Pengertian Persamaan Kuadrat atau Quadratic Equation
Persamaan kuadrat adalah bentuk persamaan matematika dengan derajat dua, sehingga mempunyai suku dengan variabel berpangkat dua. Dalam bahasa inggris persamaan kuadrat disebut dengan "Quadratic Equation". Suatu persamaan disebut persamaan kuadrat saat mempunyai suku dengan pangkat variabel tertinggi dua.
Navigasi Cepat
- A. Pengertian Persamaan Kuadrat
- B. Bentuk Umum
- C. Akar-Akar Persamaan Kuadrat
- D. Cara Menghitung Akar Persamaan Kuadrat
- E. Persamaan Kuadrat sebagai Model Non-Linier
B. Bentuk Umum Rumus Persamaan Kuadrat
Berikut bentuk umum rumus persamaan kuadrat.
dengan
a = koefisien variabel x² b = koefisien variabel x c = nilai suatu konstanta dengan a ≠ 0
Bentuk di atas juga disebut dengan bentuk kuadrat trinomial, karena mempunyai 3 istilah suku yang berbeda dalam persamaannya.
Berikut tabel contoh yang menyatakan suatu bentuk kuadrat
| Contoh | Ya/Tidak | Penjelasan |
|---|---|---|
| 2x² + 3x + 2 = 0 | Ya | a = 2; b = 3; c = 0 |
| x² + x - 1 = 0 | Ya | a = 1; b = 1; c = -1 |
| -3x² + 2 = 0 | Ya | a = -3; b = 0; c = 2 |
| 2x² + 3x = 0 | Ya | a = 2; b = 3; c = 0 |
| 3x² = 3 | Ya | berderajat 2 |
| 3x² + 4x² = 0 | Ya | berderajat 2 |
| 3x + 4 = 0 | Tidak | berderajat 1 |
| 3x² + 3x³ | Tidak | berderajat 3 |
Dari tabel di atas dapat diketahui suatu persamaan disebut persamaan kuadrat, jika persamaan tersebut berderajat dua.
Baca juga: Materi Aljabar, Bentuk Aljabar, dan Operasi Aljabar
C. Akar-Akar Persamaan Kuadrat
Akar-akar persamaan kuadrat adalah solusi penyelesaian dari suatu bentuk persamaan kuadrat, berupa nilai-nilai faktor persamaannya. Sehingga hasil substitusi akar-akarnya akan menghasilkan nilai nol terhadap persamaannya (tidak bersisa).
Persamaan kuadrat ax² + bx + c umumnya mempunyai 2 akar-akar persamaan yaitu x1 dan x2. Nilai akar-akar persamaan kuadrat di koordinat kartesius merupakan titik potong grafiknya di sumbu x. Ini dapat dibuktikan dengan substitusi nilai tersebut yang akan menghasilkan nilai nol.
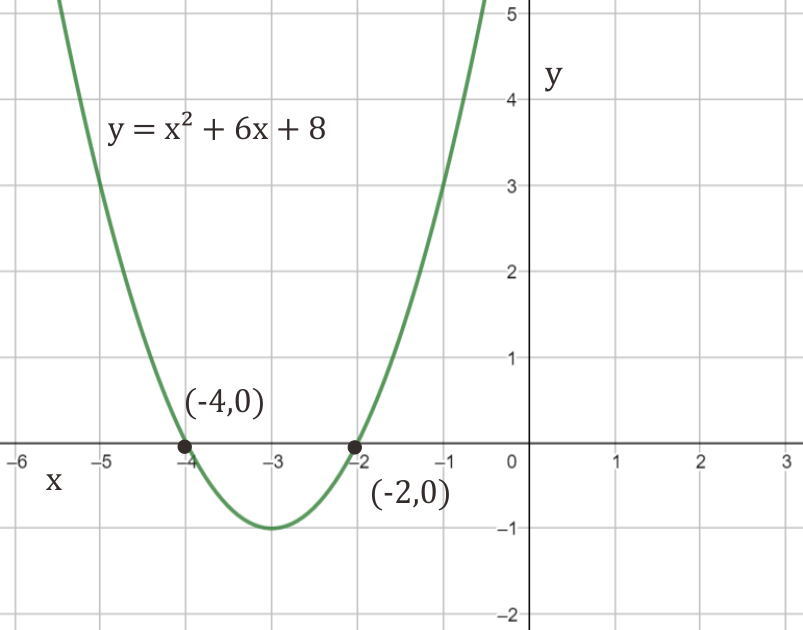
Sebagai contoh, fungsi kuadrat y = x² + 6x + 8 = 0 mempunyai akar-akar x = -4 dan x = -2. Berikut hasil substitusi nilai akar-akarnya dalam fungsi kuadrat tersebut.
Berikut substitusi nilai akar-akarnya terhadap fungsi y Substitusi x = -4 maka y = (-4)² + 6(-4) + 8 = 0 titik (-4,0) Substitusi x = -2 maka y = (-2)² + 6(-2) + 8 = 0 titik (-2,0)
D. Cara Mencari Akar Persamaan Kuadrat
Terdapat beberapa metode yang digunakan untuk mencari akar persamaan kuadrat. Berikut dijelaskan 3 metode yang sering digunakan untuk mencari akar persamaan kuadrat yaitu faktorisasi aljabar, melengkapi kuadrat sempurna, dan rumus ABC.
D1. Faktorisasi Persamaan Kuadrat
Faktorisasi persamaan kuadrat adalah dekomposisi persamaan kuadrat dengan menggunakan faktor-faktornya. Dekomposisi persamaan adalah pengubahan susunan dan struktur suatu bentuk persamaan menjadi bentuk baru yang sebanding.
Faktorisasi trinomial adalah metode umum yang digunakan untuk melakukan faktorisasi persamaan kuadrat. Metode ini bekerja dengan mencari pasangan perkalian dan penjumlahan dari nilai a, b, dan c.
Rumus Faktorisasi Bentuk Umum (Trinomial)
Terdapat beberapa bentuk kuadrat yang tidak mempunyai nilai b atau c, gunakan nilai nol dalam rumus, berikut contohnya.
| Persamaan | a | b | c |
|---|---|---|---|
| 2x² + 3x - 4 = 0 | 2 | 3 | -4 |
| 4x² + 3x = 0 | 4 | 3 | 0 |
| 25x² + 9 = 0 | 25 | 0 | 9 |
Tips: terdapat beberapa metode faktorisasi alternatif selain metode trinomial, yang dapat digunakan untuk mempercepat perhitung bentuk persamaan kuadrat tertentu.
| Faktorisasi | Contoh Persamaan Kuadrat |
|---|---|
| Bentuk Umum (Trinomial) | 6x² + 11x – 10 = (3x – 2)(2x + 5) |
| Kuadrat Murni (Pure Quadratic) | 6x² + 9x = 3x(2x + 3) |
| Selisih Kuadrat (Difference of Squares) | 9x² – 16y² = (3x – 4y)(3x + 4y) |
Lebih lanjut: Faktorisasi Trinomial, Selisih Kuadrat, dan Kuadrat Murni
# Alternatif Solusi Irasional atau Kompleks
Penggunaan metode faktorisasi dapat menjadi sulit untuk menghitung pasangan perkalian atau penjumlahan, karena solusinya merupakan bilangan irasional dan kompleks. Kasus ini dapat dipermudah dengan menggunakan metode melengkapi kuadrat sempurna atau rumus ABC yang dijelaskan di bagian bawah.
Baca juga: Apa itu Bilangan Irasional dan Bilangan Kompleks?
Contoh 1. Faktorisasi Persamaan Kuadrat x² + 6x + 8 = 0
Buat kesamaan bentuk dari persamaan kuadrat x² + 6x + 8 = 0 dan hitung akar persamaan kuadratnya!
Diketahui:
x² + 6x + 8 = 0
Ditanya:
i) Kesamaan bentuk persamaan kuadrat
ii) Menghitung akar-akar persamaan kuadrat
Penyelesaian:
x² + 6x + 8 = 0
Berdasarkan bentuk umum, dapat diketahui komponen penyusun persamaan tersebut.
a = 1, b = 6, dan c = 8
i) Kesamaan Bentuk x² + 6x + 8 = 0
Catatan: Penulisan angka 1 pada variabel x untuk memperjelas langkah, dalam praktiknya dapat tidak ditulis.
∗ Menentukan Pasangan Perkalian dan Penjumlahan
* Menghitung Nilai Pasangan Perkalian dan Penjumlahan
* Menyusun Kesamaan Bentuk Persamaan Kuadrat
∴ Jadi, kesamaan bentuknya adalah (x + 2)(x + 4) = 0
ii) Menghitung Akar Persamaan Kuadrat x² + 6x + 8 = 0
Dari pemaparan sebelumnya sudah diketahui bentuk kesamaannya berdasarkan faktorisasi yaitu (x + 2)(x + 4) = 0. Sehingga diperoleh akar-akar persamaan kuadrat dengan memecah bentuk tersebut.
∴ Jadi, akar-akar persamaan kuadrat dari x² + 6x + 8 = 0 adalah x1 = -2 dan x2 = -4.
Contoh 2. Faktorisasi Persamaan Kuadrat 2x² + 5x + 3 = 0
Buat kesamaan bentuk dari persamaan kuadrat 2x² + 5x + 3 = 0 dan hitung akar-akar penyelesaiannya!
Diketahui:
2x² + 5x + 3 = 0
Ditanya:
i) Kesamaan bentuk persamaan kuadrat
ii) Menghitung akar-akar persamaan kuadrat
Penyelesaian:
2x² + 5x + 3 = 0
Berdasarkan bentuk umum, dapat diketahui komponen penyusun persamaan tersebut
a = 2, b = 5, dan c = 3
i) Kesamaan Bentuk 2x² + 5x + 3 = 0
∗ Menentukan Pasangan Perkalian dan Penjumlahan
* Menyusun Kesamaan Bentuk Persamaan Kuadrat
∴ Jadi, kesamaan bentuknya adalah (x + 1)(2x + 3) = 0 atau (2x + 3)(x+1)
ii) Menghitung Akar Persamaan Kuadrat 2x² + 5x + 3 = 0
Dari pemaparan sebelumnya sudah diketahui bentuk kesamaannya berdasarkan faktorisasi yaitu (2x + 3)(x + 1) = 0. Sehingga diperoleh akar-akar persamaan kuadrat dengan memecah bentuk tersebut.
∴ Jadi, akar-akar persamaan kuadrat dari 2x² + 5x + 3 = 0 adalah
x1 = -1 dan x2 = -3/2.
D2. Melengkapi Kuadrat Sempurna
Melengkapi kuadrat sempurna adalah pengubahan bentuk suatu persamaan kuadrat ax2 + bx + c = 0 menjadi bentuk kuadrat sempurna a (x + d)2 + e = 0. Metode melengkapi kuadrat sempurna juga disebut dengan metode "completing the square".
Untuk melengkapi persamaan kuadrat ke kuadrat sempurna perlu dihitung nilai d dan e yang memenuhinya.
Rumus Melengkapi Kuadrat Sempurna
Sehingga dapat dihitung akar-akarnya dengan melakukan perpindahan ruas antar variabel lalu di kuadratkan.
Baca juga: Materi Melengkapi Kuadrat Sempurna dan Konsep Geometri Kuadrat Sempurna
Contoh 1. Kuadrat Sempurna dari x² + 6x + 8 = 0
Hitung akar-akar persamaan kuadrat x² + 6x + 8 = 0 dengan cara melengkapi kuadrat sempurna!
Penyelesaian:
Kemudian dapat dihitung akar-akar persamaannya dari bentuk kuadrat sempurna di atas
∴ Jadi, akar-akar persamaan kuadrat dari x² + 6x + 8 = 0 adalah x1 = -2 dan x2 = -4.
Contoh 2. Kuadrat Sempurna dari 2x² + 5x + 3 = 0
Hitung akar-akar persamaan 2x² + 5x + 3 = 0 dengan cara melengkapi kuadrat sempurna!
Penyelesaian:
Kemudian dapat dihitung akar-akar persamaannya dari bentuk kuadrat sempurna di atas
∴ Jadi, akar-akar persamaan dari 2x² + 5x + 3 = 0 adalah x1 = -1 dan x2 = -3/2.
Contoh 3. Kuadrat Sempurna dari x² + 2x - 1 = 0
Catatan: Contoh ini akan lebih sulit jika dikerjakan dengan cara faktorisasi persamaan kuadrat.
Hitung akar-akar persamaan x² + 2x - 1 = 0 dengan cara melengkapi kuadrat sempurna!
Penyelesaian:
Kemudian dapat dihitung akar-akar persamaannya dari bentuk kuadrat sempurna di atas
∴ Jadi, akar-akar persamaan dari x² + 2x - 1 = 0 adalah x1 = 0,414213562 dan x2 = -2,414213562.
D3. Rumus ABC
Rumus ABC adalah rumus alternatif untuk mencari solusi akar-akar persamaan kuadrat menggunakan nilai a, b, dan c berdasarkan konsep penyempurnaan bentuk kuadrat. Jika ditelusuri lebih lanjut, rumus ini sebenarnya merupakan hasil dari metode completing the square (melengkapi kuadrat sempurna).
Baca juga: Materi Rumus ABC, Perumusan, dan Contoh Soal
Contoh 1. Hitung Akar Persamaan x² + 6x + 8 = 0 dengan Rumus ABC!
Penyelesaian:
∴ Jadi, akar-akar persamaan kuadrat dari x² + 6x + 8 = 0 adalah x1 = -2 dan x2 = -4.
Contoh 2. Hitung Akar Persamaan x² + 2x - 1 = 0 dengan Rumus ABC!
Penyelesaian:
∴ Jadi, akar-akar persamaan kuadrat dari x² + 2x - 1 = 0 adalah x1 = 0,414213562 dan x2 = -2,414213562.
D4. Solusi Nol Persamaan Kuadrat ax² = 0
Bentuk persamaan kuadrat ax² = 0 mempunyai solusi akar bernilai nol (zero solution). Nilai solusi x1 = 0 dan x2 = 0 merupakan solusi umum persamaan kuadrat dengan bentuk ax² = 0, berikut pemaparannya.
Hal ini juga dapat dibuktikan oleh grafik fungsinya dalam koordinat kartesius, maka akan memotong sumbu koordinat di titik (0, 0). Titik ini juga menjadi titik puncak grafik yang dibentuk.
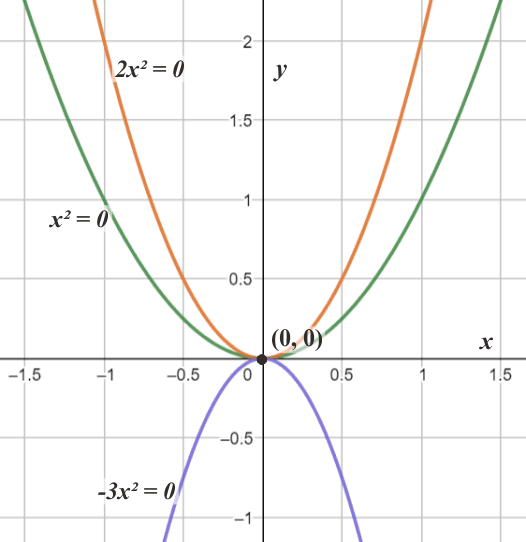
Contoh 1. Berapa solusi akar-akar persamaan kuadrat dari x² = 0; 2x² = 0; dan -3x² = 0 dan Buatkan grafik fungsinya?
Penyelesaian:
Dapat diketahui titik x = 0 menghasilkan nilai y = 0 di ketiga fungsi kuadrat yang digambarkan dalam grafik, dilihat dari ketiga grafik yang memotong titik pusat (0, 0).
∴ Jadi, akar-akar ketiga persamaan kuadrat tersebut adalah x1,2 = 0.
Lanjutan: Fungsi Kuadrat dan Cara Membuat Grafik Fungsi Kuadrat
E. Persamaan Kuadrat sebagai Pemodelan Non-Linier
Bentuk variabel berpangkat dua menyebabkan persamaan kuadrat membentuk garis tidak lurus (non-linier), umumnya berupa kurva. Pengaplikasiannya dapat dijadikan sebagai suatu model terhadap pemecahan kasus nyata. Beberapa contoh misalnya: prediksi waktu, pengaturan resistor elektronika, hukum permintaan dalam ilmu ekonomi, dan lain-lain.
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel "Persamaan Kuadrat | Rumus Umum, Akar Persamaan, & Contoh Soal". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih...