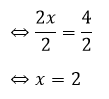A. Pengertian Sistem Persamaan Linear Satu Variabel (SPLSV)
Sistem persamaan linear satu variabel (SPLSV) adalah bentuk kalimat terbuka dari persamaan dengan satu variabel (PLSV) dalam sistem linear sebagai solusi umum dari persamaan terkait dalam sistem tersebut. Sistem ini juga sering disebut dengan SPLSV atau dalam bahasa inggris "System of Linear Equations in One Variable". Untuk memahami SPLSV diperlukan pemahaman mengenai kalimat tertutup dan terbuka
Navigasi Cepat
- A. Pengertian SPLSV
- B. Cara Penyelesaian SPLSV
- C. Contoh Soal SPLSV
- D. Contoh Soal Cerita SPLSV
A1. Kalimat Tertutup dan Terbuka
Kalimat tertutup adalah kalimat yang nilai kebenarannya selalu benar atau selalu salah. Kalimat tertutup disebut juga dengan "pernyataan" atau "closed sentence", berikut contohnya.
- 2 adalah bilangan genap (Benar)
- Ir. Soekarno adalah presiden pertama NKRI (Benar)
- 4 > 2 (Benar)
- 7 + 1 = 8 (Benar)
- 1 dibaca dua (Salah)
- Indonesia adalah sebuah provinsi (Salah)
- Everest adalah gunung terendah (Salah)
Kalimat terbuka adalah suatu kalimat yang nilai kebenarannya dapat ditentukan baik salah maupun benar. Kalimat terbuka ditandai dengan adanya variabel dalam kalimat tersebut. Kalimat terbuka dalam bahasa inggris disebut dengan "closed sentence", berikut contohnya.
- "Harga buku adalah Rp 3000" merupakan kalimat terbuka, nilai kebenarannya sesuai dengan "toko dan jenis buku yang dimaksud" sehingga "harga buku" sebagai suatu variabel.
- "x = 3" merupakan kalimat terbuka, nilai kebenaran sesuai dengan "nilai variabel x" yang dimaksud.
- "n + 1 = 3" merupakan kalimat terbuka, jika variabel n = 2 maka kalimat tersebut benar karena 2 + 1 = 3, sedangkan jika variabel n = 1 maka kalimat tersebut salah karena 1 + 1 = 2.
Berikut contoh kalimat terbuka dalam bentuk persamaan linear satu variabel (PLSV) yang diterapkan dalam sistem persamaan linear satu variabel.
Misalnya harga buku adalah Rp 3000,-
Sehingga dibuat suatu kalimat terbuka dalam bentuk persamaan linear satu variabel (PLSV) sebagai berikut.
x = 3000
Berapa harga 3 buku di toko tersebut?
Sehingga dihitung kasus matematika tersebut menggunakan sistem persamaan linear satu variabel (SPLSV), sebagai berikut
Karena x = 3000, diperoleh
3x = 3 × 3000 = 9000
Jadi, harga 3 buku adalah Rp 9000,-
Lebih lanjut, sistem linear dapat memuat beberapa komponen sekaligus berupa variabel dan konstanta sebagai gambaran pernyataan yang dibicarakan. SPLSV merupakan salah satu bentuk sederhana dari sistem linear.
A2. Bentuk Umum Persamaan Linear Satu Variabel (PLSV) dalam SPLSV
Berikut bentuk umum dan ciri-ciri persamaan linear satu variabel.
ax + b = 0
dengan:
- a merupakan koefisien variabel x
- x merupakan variabel dari PLSV. Satu variabel berarti dalam persamaan hanya terdapat 1 variabel, misalnya x. Beberapa persamaan dapat memuat lebih dari 1 suku dengan variabel x; misalnya 2x + 2 = 3x + 3
- b merupakan sebuah konstanta di ruas kiri
- Konstanta 0 pada salah satu ruas merupakan bentuk solusi umum dari fungsi persamaan linear (sebagai konsep dasar). Namun, tidak semua persamaan linear ditulis seperti ini.
Baca juga: Aljabar, Bentuk Aljabar, dan Operasi Aljabar
Catatan: Bentuk umum suatu fungsi persamaan adalah ekuivalen dengan 0 atau "Zero of Function". Pemahaman ini akan digunakan di tingkat pembelajaran yang lebih tinggi.
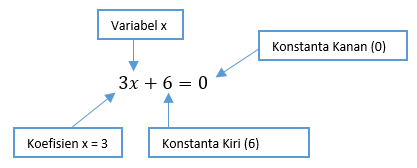
A3. Contoh Bentuk Umum PLSV dan Elemen Pembentuknya
Berikut contoh PLSV dan elemen pembentuknya.
Alasan: Persamaan "3x + 6 = 0" merupakan bentuk PLSV karena hanya terdiri dari 1 variabel, yaitu variabel "x".
B. Cara Penyelesaian Persamaan Linear Satu Variabel (SPLSV)
Cara penyelesaian SPLSV adalah menghitung nilai numerik dari variabel-nya dengan memisahkan variabel dan konstanta sehingga masing-masing ruas hanya memuat variabel dan konstanta (tidak keduanya). Berikut cara penyelesaian sistem persamaan linear satu variabel.
-
Memindahkan suatu elemen ke ruas lainnya artinya memberikan nilai lawan dari elemen tersebut ke ruas lainnya
Misalnya suatu persamaan 2x + 1 = 2, akan dipindahkan konstanta 1 di ruas kiri ke kanan.
2x + 1 = 5 (i) ⇔ 2x = 5 + (-1) (ii) ⇔ 2x = 5 - 1 (iii) ⇔ 2x = 4 (iv) terlihat pada langkah (ii) di ruas kanan ditambahkan dengan nilai -1 yang merupakan lawan dari konstanta 1 di ruas kiri.
Catatan: Tanda ⇔ merupakan operator logika ekuivalen, menyatakan bentuk semua persamaan di atas mempunyai solusi penyelesaian yang sama. # Mengapa hal ini terjadi? Sebenarnya untuk memindahkan suatu elemen dilakukan penghapusan nilai di ruas persamaan yang memuat elemen tersebut. Karena merupakan bentuk persamaan, jika terjadi penghapusan maka kedua ruas harus dilakukan penghapusan. Berikut dasar logikanya. 2x + 1 = 5 ⇔ 2x + 1 - 1 = 5 - 1 ⇔ 2x + 0 = 5 - 1 ⇔ 2x = 5 - 1 # Ingat mengurangkan sama artinya dengan menjumlahkan dengan angka negatif. 2x = 5 - 1 ⇔ 2x = 5 + (-1) Sehingga untuk mempercepat perhitungan, dapat langsung memberikan nilai lawannya. 2x + 1 = 5 ⇔ 2x = 5 - 1 ⇔ 2x = 4 -
Perhitungan nilai variabel dilakukan dengan membagi setiap ruas dengan koefisien variabel-nya
Setelah masing-masing ruas disesuaikan sehingga masing-masing ruas hanya memuat variabel dan konstanta (tidak keduanya), baru perhitungan nilai variabel dilakukan. Hal ini dilakukan dengan membagi masing-masing ruas dengan nilai koefisien variabel yang dihitung.
Misalnya kelanjutan dari langkah sebelumnya telah ditemukan 2x = 4
Dilanjutkan dengan menghitung nilai x
Karena koefisien x adalah 2, masing-masing ruas dibagi dengan 2
2x = 4
Sehingga solusi persamaan adalah nilai x = 2 -
Memindahkan elemen variabel dilakukan secara menyeluruh termasuk koefisien-nya
Untuk memindahkan suatu variabel ke ruas lainnya, nilai koefisien variabel juga ikut dipindahkan.
Misalnya akan dipindahkan variabel x ke ruas lainnya dari persamaan
3x = 2x + 1
⇔ 3x - 2x = 1
⇔ x = 1
Jadi, solusi persamaan di atas adalah x = 1
C. Contoh Soal SPLSV
Berikut contoh soal SPLSV dan penyelesaiannya. Untuk memastikan solusi yang ditemukan benar, dapat dilakukan pengujian dengan substitusi (memasukkan) nilai x ke persamaan.
-
Tentukan solusi dari sistem persamaan linear 3x - 4 = 2
Jawaban: Solusi persamaan tersebut adalah x = 2
Untuk memastikan solusi yang diperoleh benar,
jika x = 2, maka substitusi 3x - 4 = 2 sebagai berikut
3x - 4 = 2
3.(2) - 4 = 2
6 - 4 = 2
2 = 2 (Benar) -
Tentukan solusi dari sistem persamaan linear x + 3 = 2x + 6
Jawaban: Solusi persamaan tersebut adalah x = -3
Untuk memastikan solusi yang diperoleh benar,
jika x = -3, maka substitusi x + 3 = 2x + 6 sebagai berikut
x + 3 = 2x + 6
(-3) + 3 = 2.(-3) + 6
0 = -6 + 6
0 = 0 (Benar)
Baca juga: Grafik Persamaan Linear Satu Variabel
D. Contoh Soal Cerita SPLSV
Eddy membeli 3 buku tulis dan sebuah pensil. Diketahui harga pensil adalah Rp 2.000 dan total belanja Rp 11.000. Hitunglah harga sebuah buku yang dibeli Eddy?
Diketahui:
3 Buku = 3x
Pensil = Rp 2.000
Total = Rp 11.000
Penyelesaian:
Dari informasi yang ada ditemukan satu variabel buku yaitu x yang akan dicari. Sehingga dapat digunakan sistem persamaan linear satu variabel pada permasalahan di atas.
3 Buku + Pensil = Total
3x + Rp 2.000 = Rp 11.000
3x = Rp 11.000 - Rp 2.000
3x = Rp 9.000
(3x)/3 = Rp 9.000/3
x = Rp 3.000
Buku = Rp 3.000
Jawaban: Harga buku yang dibeli Eddy adalah Rp 3.000 per buah
Untuk memastikan harga buku, dapat dilakukan substitusi harga buku
3 Buku + Pensil = Total
(3 × Rp 3.000) + Rp 2.000 = Rp 11.000
Rp 9.000 + Rp 2.000 = Rp 11.000
Rp 11.000 = Rp 11.000 (Benar)
Tutorial lainnya: Daftar Isi Pelajaran Matematika
Sekian artikel "SPLSV dan Contoh Soalnya". Nantikan artikel menarik lainnya dan mohon kesediaannya untuk share dan juga menyukai halaman Advernesia. Terima kasih ...