Seperti tutorial sebelumnya mengenai Operasi Aritmatika pada MATLAB yang membahas skalar, pada tutorial ini membahas matriks sebagai objek utama. Berbeda dengan skalar yang berukuran 1 x 1, pada Operasi Matriks Menggunakan MATLAB sedikit berbeda. Anda juga perlu mengetahui dasar dari Operasi Matriks dan Aljabar Linear serta cara melakukan Addressing Array untuk mempermudah anda memahami lebih lanjut.
A. Penjumlahan (Addition) Matriks
Penjumlahan pada matriks dapat didefinisikan sebagai berikut,
Misalkan diketahui matriks A dan B, kemudian anda akan mencari nilai A+B
Anda dapat menggunakan syntax berikut
» A = [1 2; 3 4]; B = [5 6; 7 8];
» A+B
ans =
6 8
10 12B. Pengurangan (Subtraction) Matriks
Pengurangan pada matriks dapat didefinisikan sebagai berikut
Misalkan diketahui matriks C dan D, kemudian anda akan mencari nilai C-D
Anda dapat menggunakan syntax berikut
» C = [7 29; 0 1]; D = [6 4; 11 9];
» C-D
ans =
1 25
-11 -8ukuran matriks yang akan dioperasikan dengan penjumlahan dan pengurangan harus sama.
C. Perkalian (Multiplication) Matriks
Matriks dapat dilakukan operasi perkalian baik dengan skalar maupun vektor
-
Perkalian matriks dengan skalar
Berdasarkan definisi perkalian matriks A dengan skalar c menghasilkan (product) cA yang disebut kelipatan skalar (skalar multiple) matriks A.
Misalkan diketahui suatu skalar dan matriks kemudian dihitung kelipatan skalar matriks tersebut
Anda dapat menggunakan syntax berikut
» a = 7; B = [3 6; -3 8; 0 9]; » a*B ans = 21 42 -21 56 0 63 -
Perkalian matriks dengan matriks
Berdasarkan definisi hasil perkalian matriks A berukuran m x r dengan matriks B berukuran r x n adalah matriks AB berukuran m x n yang entri-entri ditentukan dari hasil kali entri baris A dengan kolom B yang bersesuaian lalu dijumlahkan. Dapat dirumuskan sebagai berikut
Misalkan diketahui matriks A dan B, yang kemudian dihitung hasil kalinya
Anda dapat menggunakan syntax berikut untuk menghitungnya dengan cepat
» A=[12 16 28; 43 78 45]; B=[72 67; 97 23; 12 45]; » A*B ans = 2752 2432 11202 6700Perlu diketahui untuk perkalian matriks A dengan B, ukuran baris A harus sama dengan ukuran kolom B.
D. Pembagian Matriks (Array Division)
Pembagian Matriks pada MATLAB menggunakan fundamental dari aljabar linear. Sebelum ke Array Division perlu diketahui tentang
-
Matriks Identitas
Matriks identitas adalah matriks persegi yang diagonal utamanya adalah 1 dan elemen lainnya adalah 0. Untuk membuat matriks diagonal pada MATLAB dapat dilihat pada tutorial Cara Membuat Matriks dengan Menggunakan MATLAB. Dalam konsep aljabar linear setiap matriks yang dikalikan matriks identitas hasilnya matriks itu sendiri.
-
Invers Matriks
Invers matriks A dapat didefinisikan sebagai matriks bujur sangkar B sedemikian hingga matriks A dioperasikan A x B = B x A = I, dimana I adalah matriks Identitas. Sedemikian B disimbolkan dengan
Anda dapat mencari invers suatu matriks menggunakan syntax inv(variabel) menggunakan MATLAB. Misalkan anda akan mencari invers matriks A yang didefinisikan sebagai berikut
» A=[3 5; 1 2] A = 3 5 1 2 » B=inv(A) B = 2.0000 -5.0000 -1.0000 3.0000 -
Determinan Matriks
Determinan matriks adalah fungsi khusus yang mengasosiasikan suatu bilangan real dengan suatu matriks bujur sangkar. Determinan matriks MATLAB menggunakan fundamental aljabar liner sebagai konsep dasarnya. Untuk menghitung determinan suatu matriks berukuran mxn anda dapat menggunakan syntax det(variabel). Misalkan anda akan menghitung determinan matriks E yang berukuran 5 x 5
» E = [1 2 3 4 5; 6 7 8 9 1; 1 2 3 3 4; 1 2 6 7 8; 1 4 7 9 8] E = 1 2 3 4 5 6 7 8 9 1 1 2 3 3 4 1 2 6 7 8 1 4 7 9 8 » det_E = det(E) det_E = 114
MATLAB mempunyai 2 jenis pembagian yaitu right division (/) dan left division(\).
Right Division
Misalkan anda mempunyai matriks A dibagi dengan matriks B menghasilkan matriks C dapat dirumuskan sebagai berikut
Misalkan diketahui
Sehingga nilai C dapat dihitung dengan syntax berikut
» A=[1 2; 3 4];B = [6 7; 8 9];
» A/B
ans =
3.5000 -2.5000
2.5000 -1.5000Left Division
Misalkan anda mempunyai matriks D dibagi dengan matriks E menghasilkan matriks F dapat dirumuskan sebagai berikut
Misalkan diketahui
Sehingga nilai F adalah
» D = [1 1; 3 2]; E=[4 5; 7 8];
» D\E
ans =
-1 -2
5 7Baca juga tutorial lainnya: Daftar Isi Tutorial MATLAB
Sekian artikel Operasi Matriks Menggunakan MATLAB. Nantikan artikel menarik lainnya dan jangan lupa share artikel ini ke kerabat anda. Terima kasih…


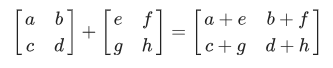
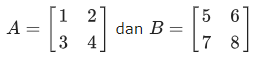
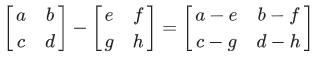
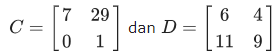
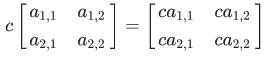
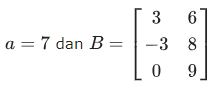
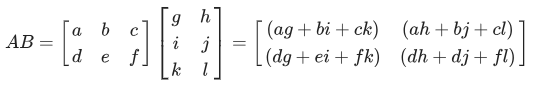
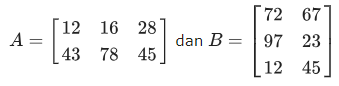
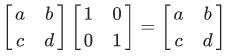
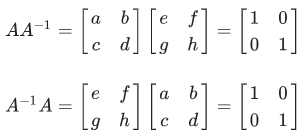
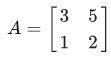
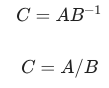
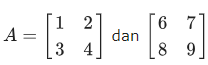
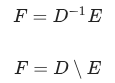
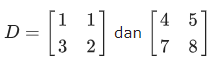












F(x)= sin (x), kedalam deret Taylor Xo=1, sampai 10 deret terakhir
TOLONG APAKAH ADA YG TAU CARA NYA MENGGUNAKAN APLIKASI MATLB